序言
符号对象(Symbolic Objects 不同于普通的数值计算)是Matlab中的一种特殊数据类型,它可以用来表示符号变量、表达式以及矩阵,利用符号对象能够在不考虑符号所对应的具体数值的情况下能够进行代数分析和符号计算(symbolic math operations),例如解代数方程、微分方程、进行矩阵运算等. 符号对象需要通过sym或syms函数来指定, 普通的数字转换成符号类型后也可以被作为符号对象来处理. 我们可以用一个简单的例子来表明数值计算和符号计算的区别: 2/5+1/3的结果为07333(double类型数值运算), 而sym(2)/sym(5)+sym(1)/sym(3)的结果为11/15, 且这里11/15仍然是属于sym类型, 是符号数.
正文
1. 符号对象的定义
符号对象的定义用syms x y z; 的形式,例如
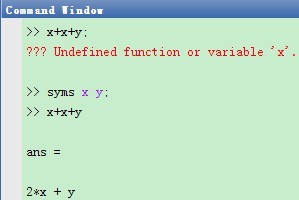
此外,还可以用x=sym('x'); y=sym('y'); 的格式定义符号变量,它跟syms x y; 具有相同的含义. Matlab也支持一次性定义一个符号表达式,如f=sym('a*x^2+b*x+c'),定义后这个表达式会被认为是一个整体,Matlab不会自动把其中每个项a,x,b ,c 定义为符号变量. 所以如果想对一个符号表达式进行计算,则还是要把参与计算的项单独定义好.
2. 符号数
Matlab支持将一个数字转换成符号对象,转换得到的符号数(Symbolic Numbers)仍然具有数字值的含义,只是之后Matlab不会对它进行浮点运算. 符号数的定义也通过sym命令实现. 例如可以让Matlab进行分数运算1/2+1/3=5/6,

而如果直接在命令窗口中输入1/2+1/3则会得到0.8333的结果. 符号数的计算比浮点计算要花费更多的时间和空间, 但是它是一种精确计算, 没有误差.
3. 符号计算
利用符号变量可以构建符号表达式、符号函数、符号方程和符号矩阵等,然后可以进行因式分解、求导、求方程、求矩阵函数值的解等操作.
(1) 因式分解Factoring
对符号表达式f进行因式分解的命令格式为factor(f). 例如将表达式(x^9-1)分解成多个因式的命令为
syms x; factor(x^9-1)
运行结果为
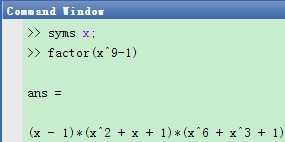
(2) 求导/求微分Differentiation
对符号表达式f(x)求导的命令为diff(f). Matlab可以自动识别表达式中的变量, 如果表达式a只包含一个变量, 则diff(f)函数是相对这个唯一的变量求导, 若a包含多个变量, 则diff(f)是对f中的默认变量求导, 默认变量是f中含有的在字母表中离x最近的变量. 表达式f的默认变量可以用函数findsym(f,1)来得出.
如果要对f(x)求n阶导数, 则用diff(f,n). 对于含有多个自变量的表达式, diff可以实现求偏导, 例如表达式f(s,t)相对s求偏导就用diff(f,s), 如果相对s求2阶偏导则是diff(f,s,2).
(3) 求积分Integral
求符号表达式f(x)的不定积分用int(f). 对于含有多个符号变量的表达式f(x,s,t), 如果希望将其相对t求积分, 用int(f,t). 求f(x)从0到1的定积分用int(f,0,1)或int(f,x,0,1).
(4) 求极限Limits
求函数f(x)或f(x,y)在x趋近于0时的极限用limit(f,x,0), 求(1+x/n)n在n趋近无穷大时的极限用limit((1+x/n)^n,n,inf), 求a(x)在x趋近0-(左极限)或x趋近0+(右极限)的时候用limit(f,x,0,'left')或limit(f,x,0,'right').
(5) 符号累加Symbolic Summation
普通的算术累加用sum, 而符号数或符号表达式的累加用symsum. 例如求1+1/22+1/32+...和1+x+x2+...用如下代码
syms x k; s1=symsum(1/k^2,1,inf) s2=symsum(x^k,k,0,inf)
(6) 符号表达式化简Simplification
利用MATLAB提供的若干表达式变形函数, 我们可以将符号表达式化简或根据需求转换成不同的形式.
- collect 可以将表达式按照其默认的符号变量的幂次由高到低排列, 同一幂次的符号变量的系数被合并到一起. 如果表达式含有多个变量, 则可以利用第二个参数指出以哪个变量为准. 例如对于f=x^3*y+x*(y^2+6)+x*y+8*x^2+y^2*x, collect(f)的结果为x^3*y+8*x^2+(2*y^2+6+y)*x, collect(f,y)的结果为2*y^2*x+(x+x^3)*y+8*x^2+6*x.
- expand 将表达式展开, 并且会应用一些基本公式(等式identities). 例如expand((x-1)*(x-2)*(x-3))的结果为x^3-6*x^2+11*x-6; expand(exp(a+b))的结果为exp(a)*exp(b); expand(cos(x+y))的结果为cos(x)*cos(y)-sin(x)*sin(y); expand(cos(3*acos(x)))的结果为4*x^3-3*x.
- horner 将表达式分解成嵌套形式. 例如horner(x^3-6*x^2+11*x-6)的结果为-6+(11+(-6+x)*x)*x.
- factor 因式分解, 将表达式分解成几个因式的乘积, 如果表达式无法分解成积的形式, 则分解结果为原表达式保持不变.
- simplify 利用各种内置的基本公式(algebraic identities)对表达式化简.
- simple 通过不同的方式对表达式进行化简, 试图得到最短的结果(结果表达式含有最少的字符数).
(7) 解代数方程
解代数方程的a(x)=0的命令是solve(a),例如

(8) 求符号矩阵的函数值
符号矩阵是指矩阵元素包含符号变量的矩阵,对这种类型的矩阵可以按照正常数值矩阵一样的规律进行计算,例如 
(8) 其他符号函数
- numden求符号分数的(消去最大公约数之后的)分子和分母。例如[n,d] = numden(sym(6/8)) 返回 n = 3 和 d = 4,单纯的numden(6/8)仅返回分子3.