一、相关类
MCvMoments
inv_sqrt_m00 m00!=0?1/sqrt(m00):0
m00 spatial moments
m01, m02, m03, m10, m11
m12, m21, m30, mu02, mu03
mu11, mu12, mu20, mu21, mu30
MCvHuMoments
hu1 Hu ivnariants
hu2, hu3, hu4, hu5, hu6, hu7
public static void cvMoments(
IntPtr arr, //Image (1-channel or 3-channel with COI set) or polygon (CvSeq of points or a vector of points)
ref MCvMoments moments, //Pointer to returned moment state structure
int binary=0 //(For images only) If the flag is non-zero, all the zero pixel values are treated as zeroes, all the others are treated as 1s
) Calculates spatial and central moments up to the third order and writes them to moments. The moments may be used then to calculate gravity center of the shape, its area, main axises and various shape characteristics including 7 Hu invariants.
注释：用于计算Hu不变矩以及其他归一化矩
public static double cvGetSpatialMoments(
ref MCvMoments moments, //传入值，传入时必须含有值，否则无法获得特定矩
int xOrder, //x order of the retrieved moment, xOrder>=0
int yOrder //y order of the retrieved moment, yOrder >= 0 and xOrder + y_order <= 3
) Retrieves the spatial moment, which in case of image moments is defined as: M_{x_order,y_order}=sum_{x,y}(I(x,y) * x^{x_order} * y^{y_order}) where I(x,y) is the intensity of the pixel (x, y).
return value: The spatial moment
注释：用于获得特定的矩
public static double cvGetCentralMoment(
ref MCvMoments moments, //Reference to the moment state structure
int xOrder, //x order of the retrieved moment, xOrder >= 0.
int yOrder //y order of the retrieved moment, yOrder >= 0 and xOrder + y_order <= 3
) Retrieves the central moment, which in case of image moments is defined as: mu_{x_order,y_order}=sum_{x,y}(I(x,y)*(x-x_c)^{x_order} * (y-y_c)^{y_order}), where x_c=M10/M00, y_c=M01/M00 - coordinates of the gravity center
Return Value: The center moment
public static double cvGetMormalizedCentralMoment(
ref MCvMoments moments, //Reference to the moment state structure
int xOrder, //x order of the retrieved moment, xOrder >= 0.
int yOrder //y order of the retrieved moment, yOrder >= 0 and xOrder + y_order <= 3
) Retrieves normalized central moment, which in case of image moments is defined as: eta_{x_order,y_order}=mu_{x_order,y_order} / M00^{(y_order+x_order)/2+1}, where mu_{x_order,y_order} is the central moment
Return Value: The normalized center moment
public static void cvGetHuMoments(
ref MCvMoments moments, //Pointer to the moment state structure
ref MCvHuMoments huMoments //Pointer to Hu moments structure.
) Calculates seven Hu invariants
public static double cvMatchShapes(
IntPtr object1, //First contour or grayscale image
IntPtr object2, //Second contour or grayscale image
Emgu.CV.CvEnum.CONTOURS_MATCH_TYPE method, //Comparison method
double parameter //Method-specific parameter (is not used now)
) Compares two shapes.The 3 implemented methods all use Hu moments
Return Value: The result of the comparison
CV_CONTOUR_MATCH_I1: I_1(A,B)=sum_{i=1..7} abs(1/m^A_i - 1/m^B_i) where m^A_i=sign(h^A_i) log(h^A_i), m^B_i=sign(h^B_i) log(h^B_i), h^A_i, h^B_i - Hu moments of A and B, respectively
CV_CONTOURS_MATCH_I2: I_2(A,B)=sum_{i=1..7} abs(m^A_i - m^B_i) where m^A_i=sign(h^A_i) log(h^A_i), m^B_i=sign(h^B_i) log(h^B_i), h^A_i, h^B_i - Hu moments of A and B, respectively
CV_CONTOURS_MATCH_I3: I_3(A,B)=sum_{i=1..7} abs(m^A_i - m^B_i)/abs(m^A_i) where m^A_i=sign(h^A_i) log(h^A_i), m^B_i=sign(h^B_i) log(h^B_i), h^A_i, h^B_i - Hu moments of A and B, respectively
public static IntPtr cvConvexHull2(
IntPtr input, //Sequence or array of 2D points with 32-bit integer or floating-point coordinates
IntPtr hullStorage, //The destination array (CvMat*) or memory storage (CvMemStorage*) that will store the convex hull. If it is array, it should be 1d and have the same number of elements as the input array/sequence. On output the header is modified so to truncate the array downto the hull size
Emgu.CV.CvEnum.ORIENTATION orientation, //Desired orientation of convex hull: CV_CLOCKWISE or CV_COUNTER_CLOCKWISE
int returnPoints //If non-zero, the points themselves will be stored in the hull instead of indices if hull_storage is array, or pointers if hull_storage is memory storage
) The function cvConvexHull2 finds convex hull of 2D point set using Sklansky's algorithm.
Return Value: If hull_storage is memory storage, the function creates a sequence containing the hull points or pointers to them, depending on return_points value and returns the sequence on output
注释：获取轮廓的凸包。第一个参数是点的数组，这个数组是一个n行2列的矩阵，或者是一个轮廓。如果是点矩阵，点应该是32位整数型或者是浮点型。下一个参数是指向内存存储的一个指针，为结果分配内存空间。下一个参数决定了程序返回的点的排列方向。最后一个参数如果设置为1，点会被存储在返回数组中。如果设置为0，只有索引被存储在返回数组中，索引是传递给cvConvexHull2()的原始数组的索引。
public static int cvCheckContourConvexity(
IntPtr contour
) Tests whether the input contour is convex or not. The contour must be simple, i.e. without self-intersections.
Return Value: -1 if input is not valid, 1 if convex, 0 otherwise
public static IntPtr cvConvexityDefects(
IntPtr contour, //Input
IntPtr convexhull, //Convex hull obtained using cvConvexHull2 that should contain pointers or indices to the contour points, not the hull points themselves, i.e. return_points parameter in cvConvexHull2 should be 0
IntPtr storage //Container for output sequence of convexity defects. If it is NULL, contour or hull (in that order) storage is used
) Finds all convexity defects of the input contour and returns a sequence of the CvConvexityDefect structures.
注释：计算凸缺陷并返回一个缺陷的序列。为了完成这个任务，函数要求输入序列，凸包和内存空间，从这个内存空间来获得存放结果序列的内存。返回一个MCvConvexityDefect结构体的序列，其中包括一些简单的参数用来描述凸缺陷
MCvConvexityDefect
Depth //Distance between the farthest point and the convex hull
DepthPointPointer //Pointer to the farthest point from the convex hull within the defect
EndPointPointer //Pointer to the point of the contour where the defect ends
StartPointPointer //Pointer to the point of the contour where the defect begins
public static void cvCalcPGH(
IntPtr contour, //Input contour. Currently, only integer point coordinates are allowed
IntPtr hist //Calculated histogram; must be two-dimensional
) Calculates 2D pair-wise geometrical histogram (PGH), described in [Iivarinen97], for the contour. The algorithm considers every pair of the contour edges. The angle between the edges and the minimum/maximum distances are determined for every pair. To do this each of the edges in turn is taken as the base, while the function loops through all the other edges. When the base edge and any other edge are considered, the minimum and maximum distances from the points on the non-base edge and line of the base edge are selected. The angle between the edges defines the row of the histogram in which all the bins that correspond to the distance between the calculated minimum and maximum distances are incremented (that is, the histogram is transposed relatively to [Iivarninen97] definition). The histogram can be used for contour matching
二、轮廓的矩
矩是通过对轮廓上所有点进行积分运算（或者认为是求和运算）而得到的一个粗略特征。在连续情况下，图像函数为
f(x,y)，那么图像的p+q阶几何矩（标准矩）定义为：
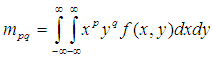p ,q = 0,1,2……
p+q阶中心距定义为：
p,q = 0,1,2……
其中
和
代表图像的重心，
,
对于离散的数字图像，采用求和号代替积分：
,
,p,q = 0,1,2 ……
N和M分别是图像的高度和宽度；
归一化的中心距定义为：
；其中
在公式中，p对应x维度上的矩，q对应y维度上的矩，阶数表示对应的部分的指数。该计算是对轮廓界上所有像素（数目为n）进行求和。如果p和q全部为0，那么m00实际上对应轮廓边界上点的数目。
虽然可以直接计算出轮廓的矩，但是经常会用到归一化的矩（因此不同大小但是形状相同的物体会有相同的值）。同样，简单的矩依赖于所选坐标系，这意味着物体旋转后就无法正确匹配。
于是就产生了Hu矩以及其他归一化矩的函数。
Hu矩是归一化中心矩的线性组合。之所以这样做是为了能够获取代表图像某个特征的矩函数。这些矩函数对缩放，旋转和镜像映射出了（h1）具有不变性。
Hu矩是从中心矩中计算得到。即七个由归一化中心矩组合成的矩:
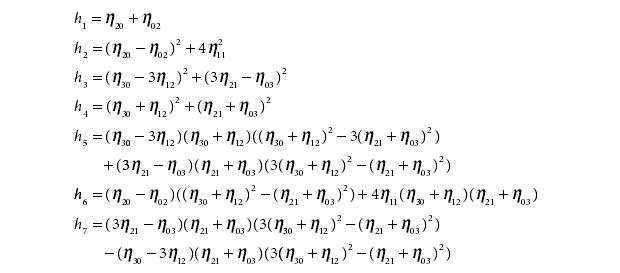
其中中心矩和归一化中心矩的定义为：
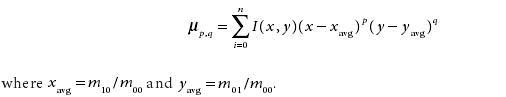
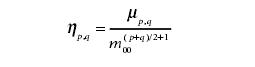
我们可以使用cvContoursMoments函数、cvMoments函数方便的得到轮廓的矩集，然后再相应的方法或函数获取各种矩。
特定的矩：cvGetSpatialMoment函数
中心矩：cvGetCentralMoment函数
归一化中心矩：cvGetNormalizedCentralMoment函数
Hu矩：cvGetHuMoments函数
三、轮廓的轮廓树
轮廓树用来描述某个特定轮廓的内部特征。注意：轮廓树跟轮廓是一一对应的关系；轮廓树不用于描述多个轮廓之间的层次关系。
轮廓树的创建过程：
从一个轮廓创建一个轮廓树是从底端（叶子节点）到顶端（根节点）的。首先搜索三角形突出或者凹陷的形状的周边（轮廓上的每一个点都不是完全和它的相邻点共线的）每个这样的三角形被一条线段代替，这条线段通过连接非相邻点的两点得到；因此实际上三角形或者被削平或者被填满。每个这样的替换都把轮廓的顶点减少，并且给轮廓树创建一个新节点。如果这样的一个三角形的两侧有原始边，那么她就是得到的轮廓树的叶子；如果一侧已是一个三角形，那么它就是那个三角形的父节点。这个过程的迭代最终把物体的外形简称一个四边形，这个四边形也被剖开；得到的两个三角形是根节点的两个子节点。
结果的二分树最终将原始轮廓的形状性比编码。每个节点被它所对应的三角形的信息所注释。
这样建立的轮廓树并不太鲁棒，因为轮廓上小的改变也可能会彻底改变结果的树，同时最初的三角形是任意选取的。为了得到较好的描述需要首先使用函数cvApproxPoly（）之后将轮廓排列（运用循环移动）成最初的三角形不怎么收到旋转影响的状态。
可以用函数cvCreateContourTree来构造轮廓树。
四、轮廓的凸包和凸缺陷
轮廓的凸包和凸缺陷用于描述物体的外形。凸包和凸缺陷很容易获得，不过我目前不知道它们到底怎么使用。
如果要判断轮廓是否是凸的，可以用cvCheckContourConvexity函数。
如果要获取轮廓的凸包，可以用cvConvexHull2函数，返回的是包含顶点的序列。
如果要获取轮廓的凸缺陷，可以用cvConvexityDefects函数。
五、轮廓的成对几何直方图
成对几何直方图（pairwise geometrical histogram PGH）是链码编码直方图（chain code histogram CCH）的一个扩展或者延伸。CCH是一种直方图，用来统计一个轮廓的Freeman链码编码每一种走法的数字。这种直方图的一个优良性质为当物体旋转45度，那么新直方图是老直方图的循环平移。这样就可以不受旋转影响。
（1）轮廓保存的是一系列的顶点，轮廓是由一系列线段组成的多边形。对于看起来光滑的轮廓（例如圆），只是线段条数比较多，线段长度比较短而已。实际上，电脑中显示的任何曲线都由线段组成。
（2）每两条线段之间都有一定的关系，包括它们（或者它们的延长线）之间的夹角，两条线段的夹角范围是：(0,180)。
（3）每两条线段上的点之间还有距离关系，包括最短（小）距离、最远（大）距离，以及平均距离。最大距离我用了一个偷懒的计算方法，我把轮廓外界矩形的对角线长度看作了最大距离。
（4）成对几何直方图所用的统计数据包括了夹角和距离。
六、轮廓的匹配
如果要比较两个物体，可供选择的特征很多。如果要判断某个人的性别，可以根据他（她）头发的长短来判断，这很直观，在长发男稀有的年代准确率也很高。也可以根据这个人尿尿的射程来判断，如果射程大于0.50米，则是男性。总之，方法很多，不一而足。
我们在上文中得到了轮廓的这么多特征，它们也可以用于进行匹配。典型的轮廓匹配方法有：Hu矩匹配、轮廓树匹配、成对几何直方图匹配。
1.Hu矩匹配
轮廓的Hu矩对包括缩放、旋转和镜像映射在内的变化具有不变性。cvMatchShapes函数可以很方便的实现对2个轮廓间的匹配。
2.轮廓树匹配
用树的形式比较两个轮廓。cvMatchContourTrees函数实现了轮廓树的对比。
3.成对几何直方图匹配
在得到轮廓的成对几何直方图之后，可以使用直方图对比的方法来进行匹。