Baum Welch估计HMM参数实例
下面的例子来自于《What is the expectation maximization algorithm?》
题面是:假设你有两枚硬币A与B,这两枚硬币抛出正面的概率分别为( heta_A)和( heta_B)。下面给出一些观测的结果,需要你去估计这两个参数( heta_A)与( heta_B)
- 假设给的数据是完整的数据,也就是样本数据告诉了你,此样本来自硬币A还是硬币B。针对与完整的数据,直接使用极大似然估计即可。具体的计算如下图所示:
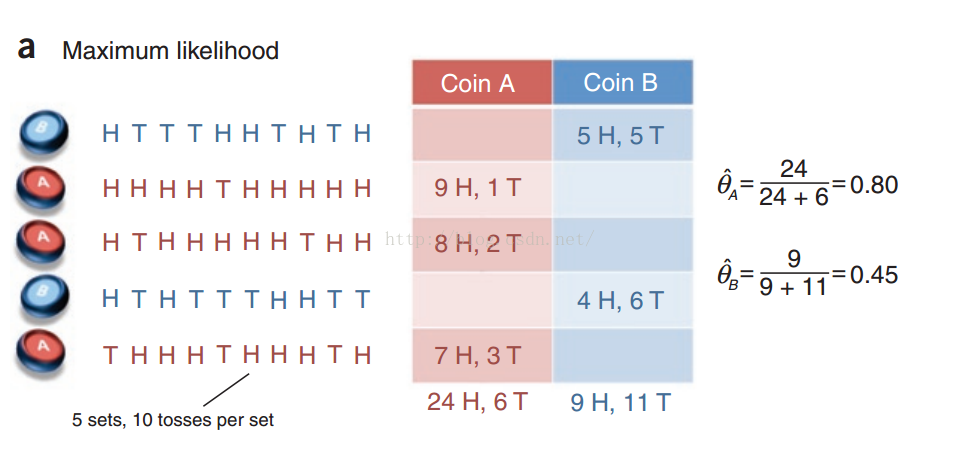
我们可以看到,整个估计的过程就是分别统计来自A的正反面与来自B的正反面,然后内部进行估计(本质上是极大似然)。
- 如果给的数据是不完整的数据呢,比如我们不知道当前观测序列是来自硬币A 还是硬币B,这个时候,就需要使用EM算法。
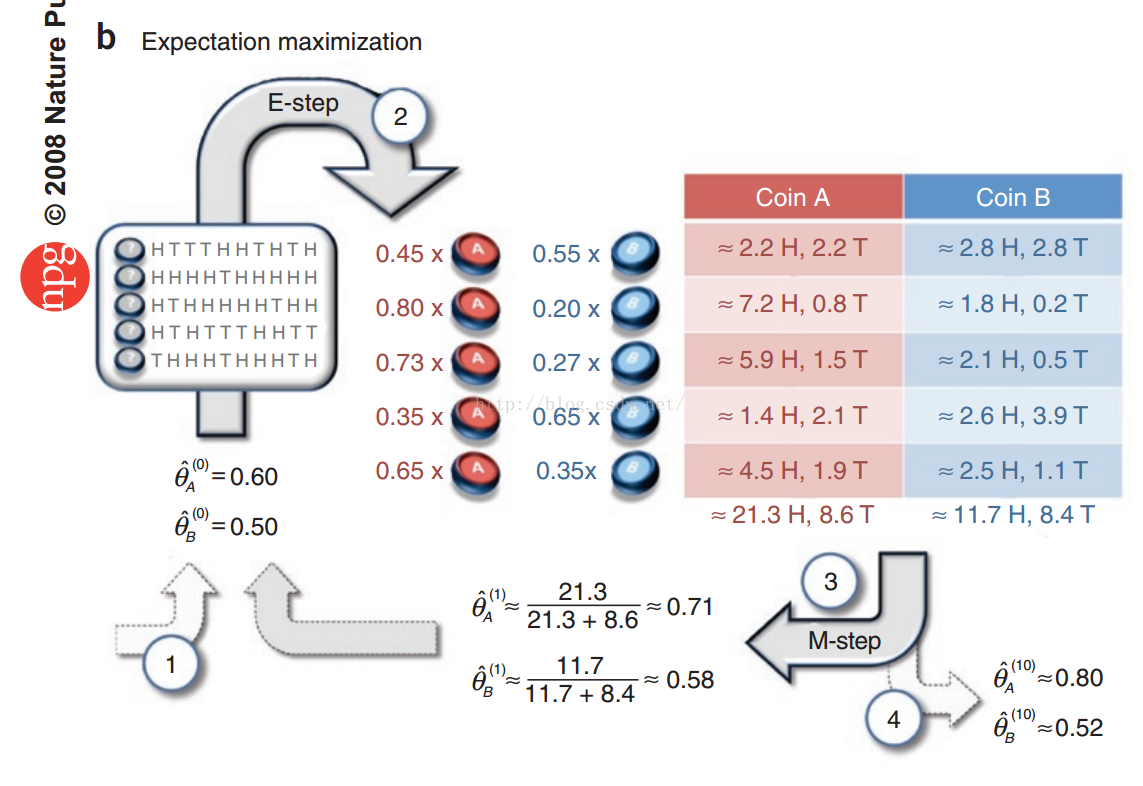
这里解释下求解的过程,首先是我们假设初始的( heta_A)与( heta_B)的值分别为 (0.6) 与 (0.5). 我们必须要知道当前样本来自A的概率与来自B的概率,然后才能得出来自A的正面期望数和来自B的正面期望数。估计很多人会被卡在这里,我也是。因为不知道图上的(0.45)等值是怎么得出来的。 实际上很简单,既然我们有了观测序列,那么我们分别计算一下来自A的似然值,然后再计算一下来自B的似然值。根据似然的大小来决定概率,具体的坐下如下
[L_A = 0.6^5 imes (1 - 0.6)^5 = 0.0007962624
]
然后再计算下来自B的似然值
[L_B = 0.5^5 imes (1 - 0.5)^5 = 0.0009765625
]
然后计算下这两个的比值,来计算来自A的概率
[P(A) = dfrac{L_A}{L_A + L_B} = 0.45
]
那么$$P(B) = 1 - P(A) = 0.55$$
然后采用上面求MLE的方法估计参数( heta_A)和参数( heta_B).
重复上述过程几次到收敛即可。