UVA1659&HDU2982->Help Little Laura 帮助小萝拉 (循环费用流)

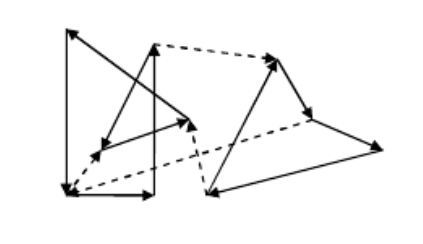
题意：平面上有m条有向线段连接了n个点。
你从某个点出发顺着有向线段行走，给走过的每条线段涂一种不同的颜色，最后回到起点。
你可以多次行走，给多个回路涂色（要么不涂色，要么就至少给一个回路上的边全部涂色）。
可以重复经过一个点，但不能重复经过一条有向线段。
如下图所示的是一种涂色方法（虚线表示未涂色，即每次都可以从任意点出发染色）。
每涂一个单位长度将得到X分，但每使用一种颜色将扣掉Y分。
假设你拥有无限多种的颜色，问如何涂色才能使得分最大？
输入保证若存在有向线段u -> v，则不会出现有向线段v -> u。
n <= 100，m <= 500，1 <= X，Y <= 1000。
对于坐标（x，y）0 <= x，y <= 1000。

思路：看刘汝佳的方法，还没有深入理解。
http://blog.csdn.net/u013368721/article/details/30553815
http://www.cnblogs.com/xcw0754/p/4659201.html

　　要求的就是最大费用循环流（即每找到一个环就可以进行增广）。找环可能并不复杂，但是要找一个最大的环就有点复杂了，所以用网络流解决。又因为找的是最大费用，按老套路的话会出现无限增大费用的情况，所以要先将每条边的费用取相反数（前面加个负），才可以有机会求最小费用流。而这些边的权有正有负，取完之后也可能出现负环了，所以主要问题就是解决负环。
　　用最小费用流求最大费用循环流时，解决负环的一种方法：
（1）先将所有边权取反。
（2）建边。正权值的边容量为1，费用为权值。负权值的边u->v拆成3条边，
分别是S->v，v->u，u->T，容量都为1，v->u费用为负权的相反数，其他2条费用为0。
这样会出现某个点有多条边连到S或T，可以互相抵消到一方为0为止，统计剩下多少条k，将其中1条的容量设为k，其他的全部删掉。如果全部抵消掉了，那就将连S和T的边全部删掉。（这个删边的方法有技巧）
（3）跑一次最小费用流得到的总费用，加上所有负权之和之后（注：此时答案已为负的），再取反即得到最大费用。

　　删边技巧是，在建这S->v，v->u，u->T 三条边时，先建中间那条，统计该点连到S几次，减去连到T点几次，结果若为正，则与S连一条边，容量就是几次，若负，同理。

　　至于why it works！得好好想想~
　　画几个点验证了一下发现，如果一个原图中的环（权值大于0）值得取，那么流会自动流向该环原图中的负权边。而如果不值得取，那么会流向原图中的正权边。因为我们是用sum（负值）加上那个费用（正值），所以当该环要取时，则自动减去那些负权，不取呢，会自动减去那些正权（而那些负权的完全没取到）。不懂就画个环出来验证吧。

===========================
一开始用lrj的vector的方法存边，TLE了一发
改成前向星存图，过了，STL还是慢啊

#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 2007;
const int INF=0x3f3f3f3f;
const double EPS = 1e-6;
struct MCMF{
    struct Edge{
        int from,to,cap,flow,nxt;
        double cost;
        Edge(){}
        Edge(int x,int y,int z,int u,double v,int n){
            from=x;to=y;cap=z;flow=u;cost=v;nxt=n;
        }
    }edges[N];
    int E,head[N];
    int n,s,t,inq[N],p[N],a[N];
    double d[N];

    inline void Init(int n,int s,int t){
        this->n = n; E = -1;
        this->s = s; this->t = t;
        memset(head,-1,sizeof(head));
    }
    inline void AddEdge(int f,int t,int c,double w){
        edges[++E] = Edge(f,t,c,0, w,head[f]);
        head[f] = E;
        edges[++E] = Edge(t,f,0,0,-w,head[t]);
        head[t] = E;
    }

    bool spfa(int s,int t,int flow,double &cost){
        for (int i=0;i<=n;i++)d[i]=INF;
        memset(inq,0,sizeof(inq));
        d[s]=0;inq[s]=1;p[s]=0;a[s]=INF;
        queue<int>Q;Q.push(s);
        for (;!Q.empty();){
            int nxt, u =Q.front();Q.pop();inq[u]=0;
            for (int i=head[u];i!=-1;i=nxt){
                Edge &e = edges[i]; nxt = e.nxt;
                if (e.cap<=e.flow||d[e.to]<=d[u]+e.cost)continue;
                d[e.to] = d[u] + e.cost;
                p[e.to] = i;
                a[e.to] = min(a[u],e.cap-e.flow);
                if (!inq[e.to]){Q.push(e.to);inq[e.to]=1;}
            }
        }
        if (d[t]==INF)return 0;//false
        flow += a[t];
        cost += (double)d[t]*(double)a[t];
        for (int u=t;u!=s;u=edges[p[u]].from){
            edges[p[u]  ].flow += a[t];
            edges[p[u]^1].flow -= a[t];
        }
        return 1;//true
    }

    //需要保证初始网络中没有负权
    double mcmf(){
        int flow =0;
        double cost = 0;
        for (;spfa(s,t,flow,cost););
        return cost;
    }//MinCostMaxFlow
} g ;

struct point{
    int x,y,d;//d:Degree
    point(){}
    inline void read(){scanf("%d%d",&x,&y);d=0;}
}po[N];
vector <int > link[N];
inline double sqr(double x){return x*x; }
inline double dist(int a,int b){
    return sqrt(sqr(po[a].x-po[b].x)+ sqr(po[a].y-po[b].y));
}

int main(){
    //freopen("in.txt","r",stdin);
    int n,dx,dy,x;
    for (int cas=0;~scanf("%d",&n)&&n;){
        scanf("%d%d",&dx,&dy);
        g.Init(n+1,0,n+1);
        for (int i=1;i<=n;i++)link[i].clear();
        for (int i=1;i<=n;i++){
            po[i].read();
            for (;~scanf("%d",&x)&&x;)link[i].push_back(x);
        }
        double ans = 0;
        for (int i=1;i<=n;i++){
            for (int j=0;j<link[i].size();j++){
                double d = dist(i,link[i][j]);
                double cost = (double)dy - 1.0*d * dx ;
                if (cost>0) g.AddEdge(i,link[i][j],1,cost);
                else {
                    ans -= cost;
                    g.AddEdge(link[i][j],i,1,-cost);
                    po[link[i][j]].d++;
                    po[i].d--;
                }
            }
        }
        for (int i=1;i<=n;i++){
            if (po[i].d>0) g.AddEdge(g.s, i, po[i].d, 0);
            if (po[i].d<0) g.AddEdge(i, g.t,-po[i].d, 0);
        }
        ans -= g.mcmf()-EPS;
        printf("Case %d: %.2lf
",++cas,ans);
    }
    return 0;
}