线段树（Segment Tree）

　　线段树也是一种可使用表结构实现的概念上的树形结构，这种方式建立过程如二叉堆中计算节点的左孩子与右孩子一样，但线段树一定是一颗完全二叉树，所以空间复杂度为 $ O(2 * n) $，$ n $ 表示数组大小。重点是要读懂线段树表示是什么意思。

　　示例：

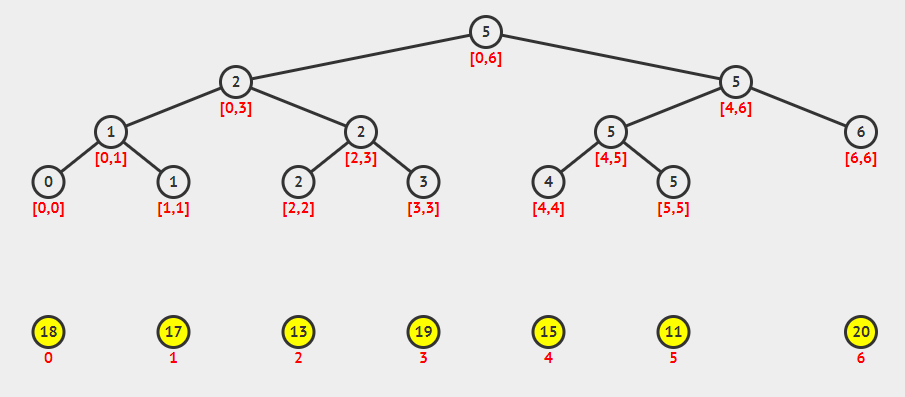
　　释义：

　　根节点 5 --- [0,6] 表示在数组 $ {18,17,13,19,15,11,20} $ 区间 [0,6] 内最小值为数组下标5的数。

　　其他节点含义同上。。。

　　下面是代码实现：

#include <iostream>
#define LC(i) ((i) << 1)
#define RC(i) ((i) << 1 | 1)
#define M 10010
#define min(a, b) ((a) < (b) ? (a) : (b))
struct { int l, r, val; } SegTree[M];
int num[] = { 18, 17, 19, 13, 15, 11, 20 };
void build(int l, int r, int k)
{
	if (l == r)
		SegTree[k].val = num[l];
	else
	{
		int m = (l + r) >> 1;
		build(l, m, LC(k));
		build(m + 1, r, RC(k));
		SegTree[k].val = min(SegTree[LC(k)].val, SegTree[RC(k)].val);
	}
}
void update(int l, int r, int k, int pos, int v)
{
	if (l > pos || r < pos || r < l)
		return;
	if (l == r)
	{
		SegTree[k].val = v;
		return;
	}
	int m = (l + r) >> 1;
	if (pos <= m)
		update(l, m, LC(k), pos, v);
	else
		update(m + 1, r, RC(k), pos, v);
	SegTree[k].val = min(SegTree[LC(k)].val, SegTree[RC(k)].val);
}
int query(int l, int r, int x, int y, int k)
{
	if (l > r || l > y || r < x)
		return M;
	if (x <= l && r <= y)
		return SegTree[k].val;
	int m = (l + r) >> 1;
	return min(query(l, m, x, y, LC(k)), query(m + 1, r, x, y, RC(k)));
}
int main()
{
	int len, x, y, k, v;

	len = (sizeof(num) / sizeof(int)) - 1;
	build(0, len, 1);

	for (int i = 1; i <= 2 * len; i++)
		std::cout << SegTree[i].val << ' ';
	std::cout << std::endl;

	std::cout << "查询[x,y]区间的最小值：" << std::endl;
	std::cin >> x >> y;
	std::cout << query(0, len, x, y, 1) << std::endl;

	std::cout << "更新下标k位置上的值：" << std::endl;
	std::cin >> k >> v;
	update(0, len, 1, k, v);

	for (int i = 1; i <= 2 * len; i++)
		std::cout << SegTree[i].val << ' ';
	std::cout << std::endl;
	return 0;
}

　　参考：

　　　　https://github.com/darkchii/cosmos/blob/master/code/data_structures/src/tree/segment_tree/segment_Tree_rmq.adb

　　　　http://www.cnblogs.com/TenosDoIt/p/3453089.html