// 此博文为迁移而来,写于2015年5月24日,不代表本人现在的观点与看法。原始地址:http://blog.sina.com.cn/s/blog_6022c4720102w1iw.html
UPDATE(20200316):重写介绍(五年前好像什么都没写一样)。
1、前言
好吧我得承认这东西应该是早就要会了的。。。虽然感觉上用的不多,但是当我开始接触AC自动机的时候,发现这是一个很必要的知识点,所以今天来讲一讲。
然而有一个问题了——为什么我一直没有搞懂就是因为许多许多次我看网上的一些文章就发现总是弄得很复杂,所以我推荐大家直接看代码,更容易弄懂。反正我就这么明白了。在AC自动机明白之后,将会有更详细地阐述。
2、介绍
KMP算法,是在普通字符串匹配算法的基础上改进的算法,核心在于:利用每次匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。首先我们先看看普通匹配算法的思路:假设读入a, b两个字符串,a为主串,b为模式串。从a的第一位起,与b的第一位起逐位匹配,直到匹配到模式串串尾。如果出现不匹配情况,则退出该次匹配,从a的第二位起,与b的第一位起逐位匹配,以此类推,即最坏匹配复杂度为O(a.len * b.len)。
KMP算法引入一个新的数组:fail数组,表示b的第i位起的子串与b本身串的最长前缀长度。例如:

同样地,你也可以理解为表示b的前i位子串的公共前后缀长度(即前缀和后缀相同)。
预处理出fail数组的意义是什么?前面提到了,每次匹配失败,我们都需要从主串第一位重新来过。
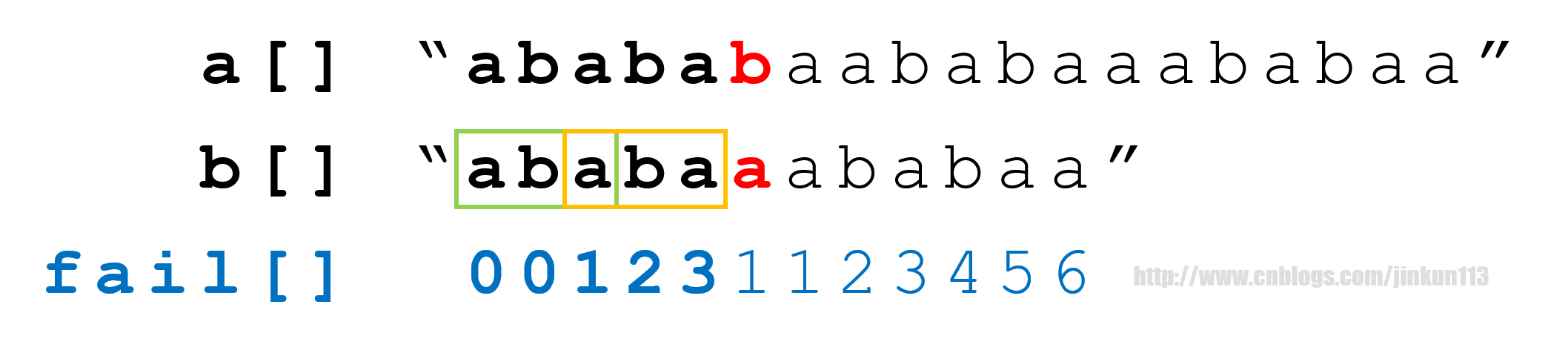
再来看一个例子,如图所示,在匹配过程中匹配到第6位时,我们发现匹配失败了;而已匹配上的前5位,其第5位的fail值为3,表示前5位的公共前后缀长度为3,也就是说,[3, 5]子串和[1, 3]子串是一致的,那我们也就不再需要对这一段进行一一匹配了,从而直接从a的第5+1=6位和b的第3+1=4位开始匹配。
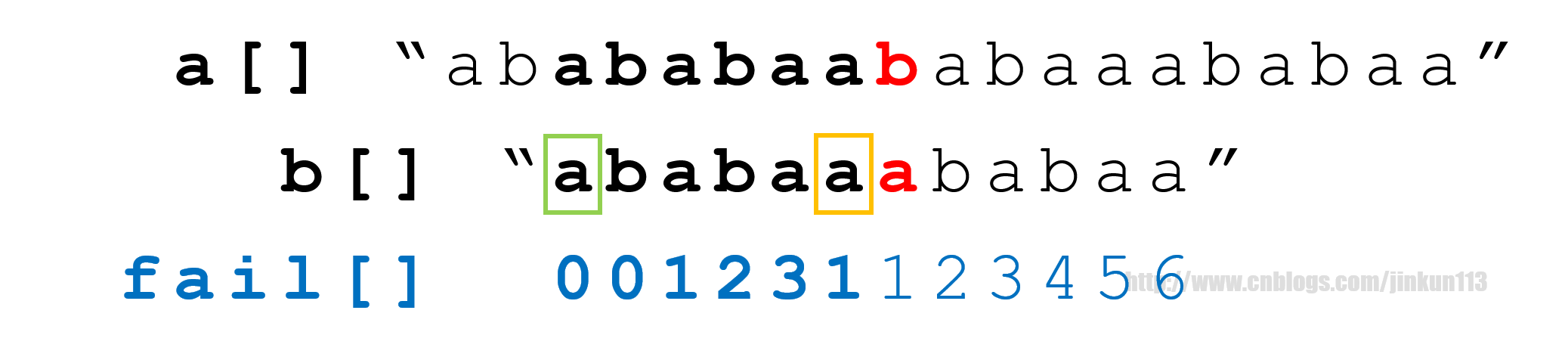
以此类推,可以理解为b串自身整体右移,使其与a串匹配,故时间复杂度约为O(a.len + b.len),大幅降低。
3、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 100005 5 6 int la, lb, fail[MAXN]; 7 char a[MAXN], b[MAXN]; 8 9 int main() { 10 cin >> a + 1 >> b + 1; 11 la = strlen(a + 1), lb = strlen(b + 1); 12 fail[0] = -1; 13 for (int i = 1, x = -1; i <= lb; i++) { 14 while (x >= 0 && b[x + 1] != b[i]) x = fail[x]; 15 fail[i] = ++x; 16 } 17 for (int i = 1, x = 0; i <= la; i++) { 18 while (x >= 0 && b[x + 1] != a[i]) x = fail[x]; 19 if (++x == lb) cout << i - lb + 1, exit(0); 20 } 21 cout << "N/A"; 22 return 0; 23 }