《DSP using MATLAB》Problem 8.40

代码：

function [wpLP, wsLP, alpha] = bs2lpfre(wpbs, wsbs)
% Band-edge frequency conversion from bandstop to lowpass digital filter
% -------------------------------------------------------------------------
% [wpLP, wsLP, alpha] = bs2lpfre(wpbs, wsbs) 
%   wpLP = passband edge for the lowpass digital prototype 
%   wsLP = stopband edge for the lowpass digital prototype 
%  alpha = lowpass to bandstop transformation parameter
%   wpbs = passband edge frequency array [wp_lower, wp_upper] for the bandstop
%   wsbs = stopband edge frequency array [ws_lower, ws_upper] for the bandstop
%
%

% Determine the digital lowpass cutoff frequencies:
wpLP = 0.2*pi;
     K = tan((wpbs(2)-wpbs(1))/2)*tan(wpLP/2);
  beta = cos((wpbs(2)+wpbs(1))/2)/cos((wpbs(2)-wpbs(1))/2);
alpha1 = -2*beta*K/(K+1);
alpha2 = (1-K)/(K+1);

alpha = [alpha1, alpha2];

wsLP = -angle((exp(-2*j*wsbs(1))+alpha1*exp(-j*wsbs(1))+alpha2)/(alpha2*exp(-2*j*wsbs(1))+alpha1*exp(-j*wsbs(1))+1))
wsLP = angle((exp(-2*j*wsbs(2))+alpha1*exp(-j*wsbs(2))+alpha2)/(alpha2*exp(-2*j*wsbs(2))+alpha1*exp(-j*wsbs(2))+1))

　　

function [b, a] = cheb1bsf(wpbs, wsbs, Rp, As)
% IIR bandstop Filter Design using Chebyshev-1 Prototype
% -----------------------------------------------------------------------
% [b, a] = cheb1bsf(wp, ws, Rp, As);
%      b = numerator polynomial coefficients of bandstop filter, Direct form
%      a = denominator polynomial coefficients of bandstop filter, Direct form
%     wp = Passband edge frequency array [wp_lower, wp_upper] in radians;
%     ws = Stopband edge frequency array [ws_lower, ws_upper] in radians;
%     Rp = Passband ripple in +dB; Rp > 0
%     As = Stopband attenuation in +dB; As > 0
%
%
% Determine the digital lowpass cutoff frequencies:
wpLP = 0.2*pi;
     K = tan((wpbs(2)-wpbs(1))/2)*tan(wpLP/2);
  beta = cos((wpbs(2)+wpbs(1))/2)/cos((wpbs(2)-wpbs(1))/2);
alpha1 = -2*beta*K/(K+1);
alpha2 = (1-K)/(K+1);

alpha = [alpha1, alpha2];

wsLP = -angle((exp(-2*j*wsbs(1))+alpha1*exp(-j*wsbs(1))+alpha2)/(alpha2*exp(-2*j*wsbs(1))+alpha1*exp(-j*wsbs(1))+1))
wsLP = angle((exp(-2*j*wsbs(2))+alpha1*exp(-j*wsbs(2))+alpha2)/(alpha2*exp(-2*j*wsbs(2))+alpha1*exp(-j*wsbs(2))+1))

% Compute Analog Lowpass Prototype Specifications: Inverse Mapping for frequencies
T = 1; Fs = 1/T;                    % set T = 1
OmegaP = (2/T)*tan(wpLP/2);         % Prewarp(Cutoff) prototype passband freq
OmegaS = (2/T)*tan(wsLP/2);         % Prewarp(cutoff) prototype stopband freq

% Design Analog Chebyshev-1 Prototype Lowpass Filter:
[cs, ds] = afd_chb1(OmegaP, OmegaS, Rp, As);

% Bilinear transformation to obtain digital lowpass:
[blp, alp] = bilinear(cs, ds, Fs);

% Transform digital lowpass into bandstop filter
Nz = [alpha2, alpha1, 1]; Dz = [1, alpha1, alpha2];
[b, a] = zmapping(blp, alp, Nz, Dz);

　　

%% ------------------------------------------------------------------------
%%            Output Info about this m-file
fprintf('
***********************************************************
');
fprintf('        <DSP using MATLAB> Problem 8.40.2 

');

banner();
%% ------------------------------------------------------------------------

% Digital Filter Specifications:   Chebyshev-1 bandstop
wsbs = [0.35*pi 0.65*pi];             % digital stopband freq in rad
wpbs = [0.25*pi 0.75*pi];             % digital passband freq in rad

delta1 = 0.05;                      % passband tolerance, absolute specs 
delta2 = 0.01;                      % stopband tolerance, absolute specs

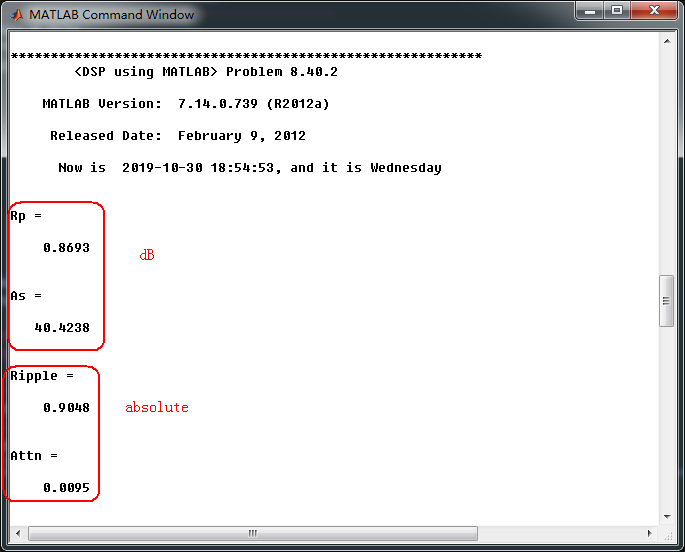
Rp = -20 * log10( (1-delta1)/(1+delta1))    % passband ripple in dB
As = -20 * log10( delta2 / (1+delta1))      % stopband attenuation in dB                       

Ripple = 10 ^ (-Rp/20)           % passband ripple in absolute
Attn = 10 ^ (-As/20)             % stopband attenuation in absolute

% --------------------------------------------------------
%         method 1:  cheb1bsf function
% --------------------------------------------------------
fprintf('
*******Digital bandstop, Coefficients of DIRECT-form***********
');
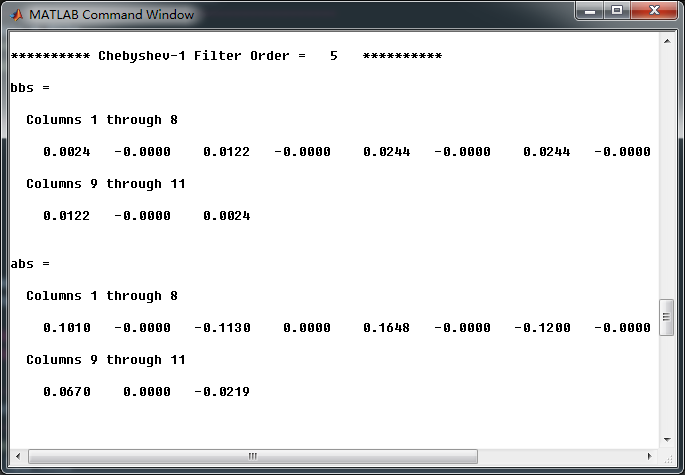
[bbs, abs] = cheb1bsf(wpbs, wsbs, Rp, As)
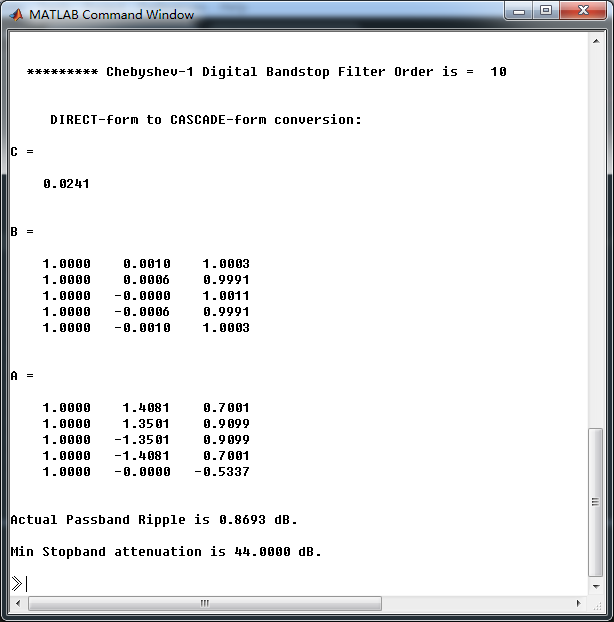
[C, B, A] = dir2cas(bbs, abs)


% Calculation of Frequency Response:

[dbbs, magbs, phabs, grdbs, wwbs] = freqz_m(bbs, abs);

% ---------------------------------------------------------------
%    find Actual Passband Ripple and Min Stopband attenuation
% ---------------------------------------------------------------
delta_w = 2*pi/1000;
Rp_bs = -(min(dbbs( 1:1:ceil(wpbs(1)/delta_w+1) )));    % Actual Passband Ripple

fprintf('
Actual Passband Ripple is %.4f dB.
', Rp_bs);

As_bs = -round(max(dbbs(ceil(wsbs(1)/delta_w)+1:1:ceil(wsbs(2)/delta_w)+1)));        % Min Stopband attenuation
fprintf('
Min Stopband attenuation is %.4f dB.

', As_bs);


%% -----------------------------------------------------------------
%%                             Plot
%% -----------------------------------------------------------------  

figure('NumberTitle', 'off', 'Name', 'Problem 8.40.2 Chebyshev-1 bs by cheb1bsf function')
set(gcf,'Color','white'); 
M = 1;                          % Omega max

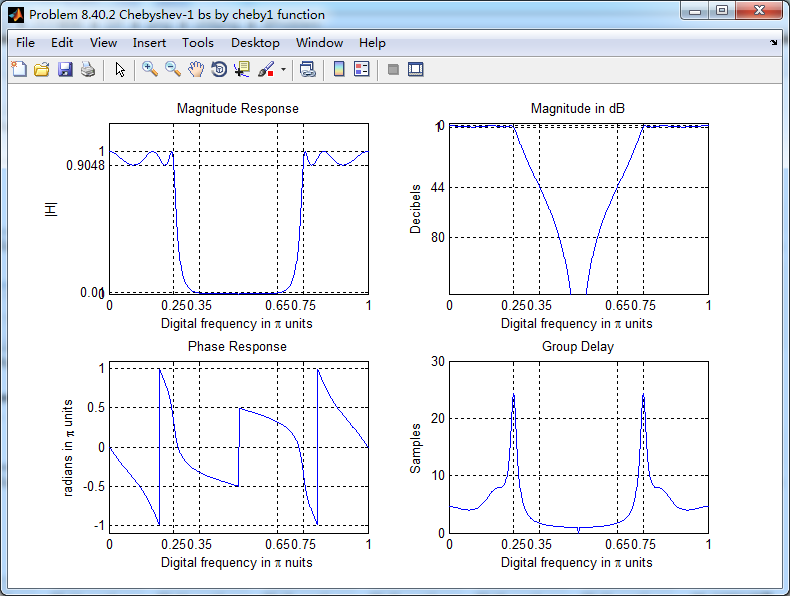
subplot(2,2,1); plot(wwbs/pi, magbs); axis([0, M, 0, 1.2]); grid on;
xlabel('Digital frequency in pi units'); ylabel('|H|'); title('Magnitude Response');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.25, 0.35, 0.65, 0.75, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.01, 0.9048, 1]);

subplot(2,2,2); plot(wwbs/pi, dbbs); axis([0, M, -100, 2]); grid on;
xlabel('Digital frequency in pi units'); ylabel('Decibels'); title('Magnitude in dB');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.25, 0.35, 0.65, 0.75, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [-80, -44, -1, 0]);
set(gca,'YTickLabelMode','manual','YTickLabel',['80'; '44';'1 ';' 0']);


subplot(2,2,3); plot(wwbs/pi, phabs/pi); axis([0, M, -1.1, 1.1]); grid on;
xlabel('Digital frequency in pi nuits'); ylabel('radians in pi units'); title('Phase Response');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.25, 0.35, 0.65, 0.75, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1:0.5:1]);

subplot(2,2,4); plot(wwbs/pi, grdbs); axis([0, M, 0, 30]); grid on;
xlabel('Digital frequency in pi units'); ylabel('Samples'); title('Group Delay');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.25, 0.35, 0.65, 0.75, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [0:10:30]);


figure('NumberTitle', 'off', 'Name', 'Problem 8.40.2 Pole-Zero Plot')
set(gcf,'Color','white'); 
zplane(bbs, abs); 
title(sprintf('Pole-Zero Plot'));
%pzplotz(b,a);





% --------------------------------------------------------------------------------
%           cheby1 function
% --------------------------------------------------------------------------------
% Calculation of Chebyshev-1 filter parameters:
[N, wn] = cheb1ord(wpbs/pi, wsbs/pi, Rp, As);

fprintf('
  ********* Chebyshev-1 Digital Bandstop Filter Order is = %3.0f 
', 2*N)

% Digital Chebyshev-1 bandstop Filter Design:
[bbs, abs] = cheby1(N, Rp, wn, 'stop');

[C, B, A] = dir2cas(bbs, abs)

% Calculation of Frequency Response:
[dbbs, magbs, phabs, grdbs, wwbs] = freqz_m(bbs, abs);

% ---------------------------------------------------------------
%    find Actual Passband Ripple and Min Stopband attenuation
% ---------------------------------------------------------------
delta_w = 2*pi/1000;
Rp_bs = -(min(dbbs(1:1:ceil(wpbs(1)/delta_w+1))));                             % Actual Passband Ripple

fprintf('
Actual Passband Ripple is %.4f dB.
', Rp_bs);

As_bs = -round(max(dbbs(ceil(wsbs(1)/delta_w)+1:1:ceil(wsbs(2)/delta_w)+1)));   % Min Stopband attenuation
fprintf('
Min Stopband attenuation is %.4f dB.

', As_bs);


%% -----------------------------------------------------------------
%%                             Plot
%% -----------------------------------------------------------------  

figure('NumberTitle', 'off', 'Name', 'Problem 8.40.2 Chebyshev-1 bs by cheby1 function')
set(gcf,'Color','white'); 
M = 1;                          % Omega max

subplot(2,2,1); plot(wwbs/pi, magbs); axis([0, M, 0, 1.2]); grid on;
xlabel('Digital frequency in pi units'); ylabel('|H|'); title('Magnitude Response');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.25, 0.35, 0.65, 0.75, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.01, 0.9048, 1]);

subplot(2,2,2); plot(wwbs/pi, dbbs); axis([0, M, -120, 2]); grid on;
xlabel('Digital frequency in pi units'); ylabel('Decibels'); title('Magnitude in dB');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.25, 0.35, 0.65, 0.75, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [-80, -44, -1, 0]);
set(gca,'YTickLabelMode','manual','YTickLabel',['80'; '44';'1 ';' 0']);


subplot(2,2,3); plot(wwbs/pi, phabs/pi); axis([0, M, -1.1, 1.1]); grid on;
xlabel('Digital frequency in pi nuits'); ylabel('radians in pi units'); title('Phase Response');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.25, 0.35, 0.65, 0.75, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1:0.5:1]);

subplot(2,2,4); plot(wwbs/pi, grdbs); axis([0, M, 0, 30]); grid on;
xlabel('Digital frequency in pi units'); ylabel('Samples'); title('Group Delay');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.25, 0.35, 0.65, 0.75, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [0:10:30]);

　　运行结果：

       通带、阻带设计指标，dB单位和绝对值单位

        采用cheb1bsf函数，得到Chebyshev-1型数字带阻滤波器，系统函数直接形式的系数如下

        转换成串联形式，系数如下

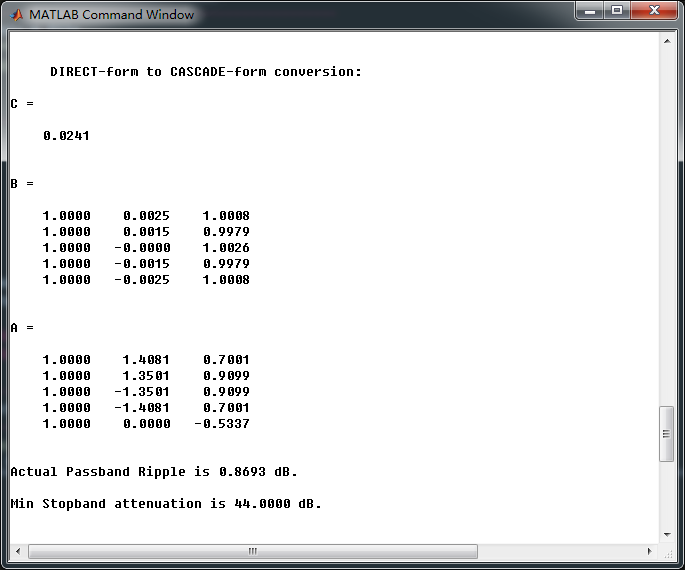
        幅度谱、相位谱和群延迟响应

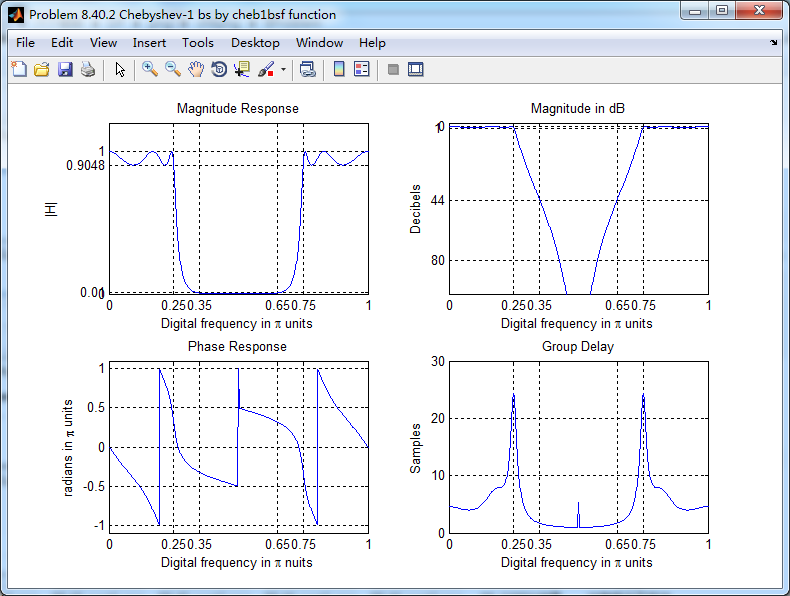
        数字带阻滤波器零极点图

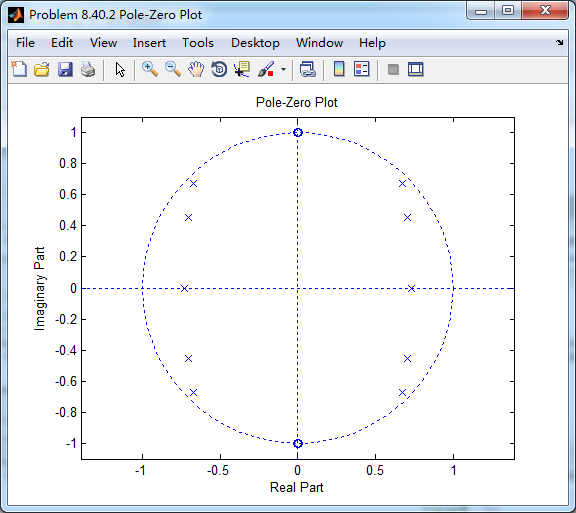
        和P8.39进行对比，采用cheby1函数（MATLAB工具箱函数），计算得到数字带阻滤波器，系统函数直接形式的系数如下