Wolsey "强整数规划“ 建模的+Leapms实践——无产能批量问题
《整数规划》[1]一书作者L. A. Wolsey对批量问题(Lot-sizing Problem)做了不少“强”整数规划建模[2-5],不是management science就是operations research,大师呀。
一个“弱”整数规划模型可以通过添加约束使之变“强” (Strong)。由于所添加的约束是线性不等式约束,就是空间上的平面并且把空间分成两半,一半留在可行解空间里,一半排除出可行解空间,于是这种约束就被叫成“割平面”(cutting plane)。
本帖记录用+Leapms对模型强化过程的实践,几乎是一个可以跟随的教程贴。如果没有+Leapms在手上,用其他建模语言和求解器也一样可以做,不过就是麻烦些。
本帖是本博客原创,本博客不转贴他人贴(除非今后说明)。
无产能批量问题(Uncapacited Lot-sizing Problem)
考虑在未来T个周期的生产-存贮问题,t (t=1,...,T) 周期的产品需求为d[t], 单位生产费用为p[t], 单位存贮费用为h[t], 生产的固定性费用为 f[t]。 要求制定生产t周期的生产量 x[t],使得总费用最少。
这里的矛盾是:如果生产过于频繁,则要付出更多的固定性费用;如果一次生产过多,则需要付出更多存贮费,且各个周期的生产费用是不同的,应该尽量避免在高生产费用的周期生产。
各个符号有英文涵义:d[t] -- demand at time t; p[t] -- production cost at time t; h[t] -- holding cost at time t; f[t] - fixed cost at time t。
假设产能是无限的,即x[t]可以取到所有d[t]的和,因此叫做无产能批量问题。
这个例子在Wolsey书的223-227页。
设$s_t$是t时间的库存,Wolse 是这样描述模型的:
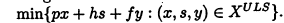
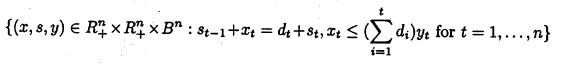
上面的第一行是说要极小化总费用;第二行是约束。熟悉+Leapms的同学知道上面的$x_t$就是x[t]了。
上面的第二行包括两个约束式,第一个是说阶段t-1的库存加上t阶段的生产等于t阶段的需求加上t阶段的库存,显然符合逻辑。就是这个:
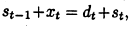
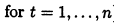
第二个是说如果在t时间内生产,则0-1变量$y_t$必须是1。这个$y_t$表示t阶段是否有生产,它要在目标里面乘上$f$, 即$fy$。
对这样的描述写成+Leapms只需要一分钟。但是写之前最好能弄些d,p,h,f的数据,否则是无本之木,没法实践。还好Wolsey给出了数据,在224页第五段:
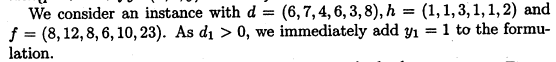
但是,Wolsey忘记给 p[t]了!发邮件给他被退回,好像老先生已经退休了。似乎实践要泡汤了。
不过思考一下没事的,因为p在研究强模型时候并不重要,只不过我们没法精准复现Wolsey的数据了,但是只要能复现模型由弱变强的性质就好。
首先我们要把“弱”模型写出来,就是这个:
min sum{t=1,...,T}(h[t]s[t]+f[t]y[t])
subject to
s[t-1]+x[t]=d[t]+s[t] | t=1,...,T
x[t]<=M*y[t]|t=1,...,T
s[0]=0
where
T,M are numbers
d,h,f are sets
s[t] is a variable of nonnegative number|t=0,...,T
x[t] is a variable of nonnegative number|t=1,...,T
y[t] is a variable of binary|t=1,...,T
data_relation
M=sum{t=1,...,T}d[t]
data
T=6 //阶段数
d={6 7 4 6 3 8}//需求
h={1 1 3 1 1 2}//单位存贮费用
f={8 12 8 6 10 23} //时间t内的生产固定费用
用+Leapms松弛求解一下:
+Leapms>solve The LP is solved to optimal. 找到线性规划最优解.非零变量值和最优目标值如下: ......... x1*=6 x2*=7 x3*=4 x4*=6 x5*=3 x6*=8 y1*=0.176471 y2*=0.205882 y3*=0.117647 y4*=0.176471 y5*=0.0882353 y6*=0.235294 ......... Objective*=12.1765 ......... +Leapms>
6个y[t]都不是整数,大体跟Wolsey的图示一致:
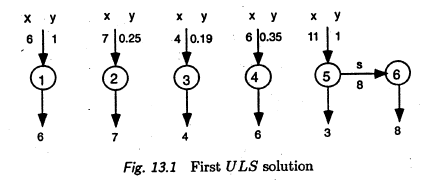
加割平面让模型变强(Strong)
加第1个割平面,原文这样写
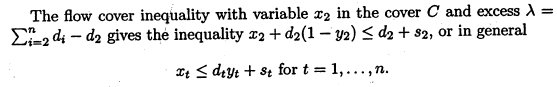
加进来的+Leapms这样写:
x[t]<=d[t]y[t]+s[t]|t=1,...,T //割平面1
加第2个割平面,原文这样写
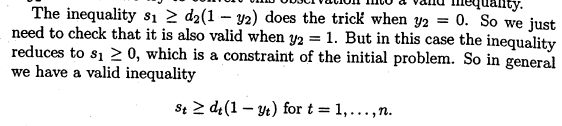
照抄写成+Leapms:
s[t]>=d[t](1-y[t])|t=1,...,T //割平面2
用+Leapms求解怪怪的!分析。。。分析。。。分析。。。
原来Wolsey写错了,正确的应该是:

重新写成+Leapms:
s[t-1]>=d[t](1-y[t])|t=1,...,T //割2
加了上面两个割平面,用+Leapms松弛求解一下看:
+Leapms>solve The LP is solved to optimal. 找到线性规划最优解.非零变量值和最优目标值如下: ......... s1*=5.96296 s2*=4 s4*=2.22581 s5*=8 x1*=11.963 x2*=5.03704 x4*=8.22581 x5*=8.77419 y1*=1 y2*=0.148148 y4*=1 y5*=0.258065 ......... Objective*=38.5472 ......... +Leapms>
可以看见,只剩下两个0-1变量 y2和y5不是整数了。看一下Wolsey的结果:
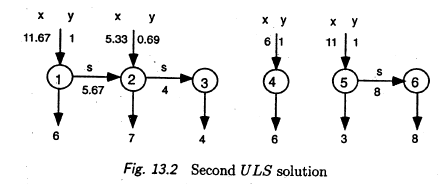
分析。。。分析。。。分析, 大体一致!
下面Wolsey还有另外两个割,他们看起来差不多,仔细看还是大不一样啊:
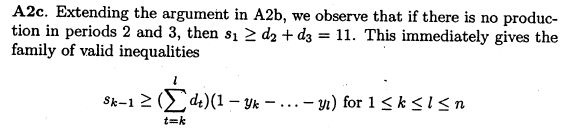
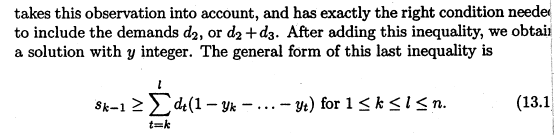
什么?这样的割也能写成+Leapms吗?
必须的!写出来是这样的:
s[k-1]>=(sum{t=k,...,l}d[t])(1-sum{i=k,...,l}y[i]) | k=1,...,T;l=1,...,T;k<=l//割平面3 s[k-1]>=sum{t=k,...,l}(d[t](1-sum{i=k,...,l}y[i])) | k=1,...,T;l=1,...,T;k<=l//割平面4
所有割都加完了,用+Leapms求解其松弛求一下吧:
+Leapms>solve The LP is solved to optimal. 找到线性规划最优解.非零变量值和最优目标值如下: ......... s1*=6.30249 s2*=2.69039 s5*=8 x1*=12.3025 x2*=3.3879 x3*=1.30961 x4*=6 x5*=11 y1*=1 y2*=0.0996441 y3*=0.327402 y4*=1 y5*=1 ......... Objective*=44.8078 ......... +Leapms>
模型确实强了不少,而且与Wolsey画出的结果大体一致:
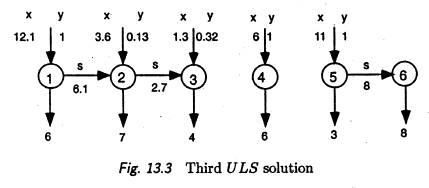
好了,实践做完了。
强模型PDF摘录
所谓强模型pdf摘录就是+Leapms自动附加生成的一个pdf文档,包含了+Leapms格式的模型和数学概念模型:

其他
问:+Leapms只能求松弛解吗?
答:当然不是。用solve命令得出的是松弛解,用mip呼叫+Leapms自身求解器得出的是整数解,用cplex命令则呼叫cplex生成整数解,用grb命令。。。。
问:上面PDF中的数学公式是+Leapms自动生成的吗?
答:当然是。
问:+Leapms能生成MPS模型吗?
答:当然能,用savemps命令就行。
问:+Leapms能生成lp格式模型吗?
答:当然能,用savelp命令就行。
问:那么能否让+Leapms生成其他建模语言模型?
答:当然能,很神奇。
附录1:+Leapms生成的lp模型
================================== Problem UncapacitatedLotSizingStrong .lp file gnerated by +Leapms ================================== Minimize Obj: s1+s2+3s3+s4+s5+2s6+8y1+12y2+8y3+6y4+10y5+23y6 Subject to C1: s0-s1+x1=6 C2: s1-s2+x2=7 C3: s2-s3+x3=4 C4: s3-s4+x4=6 C5: s4-s5+x5=3 C6: s5-s6+x6=8 C7: x1-34y1<=-0 C8: x2-34y2<=-0 C9: x3-34y3<=-0 C10: x4-34y4<=-0 C11: x5-34y5<=-0 C12: x6-34y6<=-0 C13: s0=-0 C14: -s1+x1-6y1<=-0 C15: -s2+x2-7y2<=-0 C16: -s3+x3-4y3<=-0 C17: -s4+x4-6y4<=-0 C18: -s5+x5-3y5<=-0 C19: -s6+x6-8y6<=-0 C20: s0+6y1>=6 C21: s1+7y2>=7 C22: s2+4y3>=4 C23: s3+6y4>=6 C24: s4+3y5>=3 C25: s5+8y6>=8 C26: s0+6y1>=6 C27: s0+13y1+13y2>=13 C28: s0+17y1+17y2+17y3>=17 C29: s0+23y1+23y2+23y3+23y4>=23 C30: s0+26y1+26y2+26y3+26y4+26y5>=26 C31: s0+34y1+34y2+34y3+34y4+34y5+34y6>=34 C32: s1+7y2>=7 C33: s1+11y2+11y3>=11 C34: s1+17y2+17y3+17y4>=17 C35: s1+20y2+20y3+20y4+20y5>=20 C36: s1+28y2+28y3+28y4+28y5+28y6>=28 C37: s2+4y3>=4 C38: s2+10y3+10y4>=10 C39: s2+13y3+13y4+13y5>=13 C40: s2+21y3+21y4+21y5+21y6>=21 C41: s3+6y4>=6 C42: s3+9y4+9y5>=9 C43: s3+17y4+17y5+17y6>=17 C44: s4+3y5>=3 C45: s4+11y5+11y6>=11 C46: s5+8y6>=8 C47: s0+6y1>=6 C48: s0+13y1+13y2>=13 C49: s0+17y1+17y2+17y3>=17 C50: s0+23y1+23y2+23y3+23y4>=23 C51: s0+26y1+26y2+26y3+26y4+26y5>=26 C52: s0+34y1+34y2+34y3+34y4+34y5+34y6>=34 C53: s1+7y2>=7 C54: s1+11y2+11y3>=11 C55: s1+17y2+17y3+17y4>=17 C56: s1+20y2+20y3+20y4+20y5>=20 C57: s1+28y2+28y3+28y4+28y5+28y6>=28 C58: s2+4y3>=4 C59: s2+10y3+10y4>=10 C60: s2+13y3+13y4+13y5>=13 C61: s2+21y3+21y4+21y5+21y6>=21 C62: s3+6y4>=6 C63: s3+9y4+9y5>=9 C64: s3+17y4+17y5+17y6>=17 C65: s4+3y5>=3 C66: s4+11y5+11y6>=11 C67: s5+8y6>=8 Binaries y1 y2 y3 y4 y5 y6 End ==================================
附录2 MPS模型
MPS是机器交换模型,不是给人看的。供参考。
*MPS FILE GENERATED FROM +LEAPMS NAME UncapacitatedLotSizingStrong ROWS N OBJCT E C1 E C2 E C3 E C4 E C5 E C6 L C7 L C8 L C9 L C10 L C11 L C12 E C13 L C14 L C15 L C16 L C17 L C18 L C19 G C20 G C21 G C22 G C23 G C24 G C25 G C26 G C27 G C28 G C29 G C30 G C31 G C32 G C33 G C34 G C35 G C36 G C37 G C38 G C39 G C40 G C41 G C42 G C43 G C44 G C45 G C46 G C47 G C48 G C49 G C50 G C51 G C52 G C53 G C54 G C55 G C56 G C57 G C58 G C59 G C60 G C61 G C62 G C63 G C64 G C65 G C66 G C67 COLUMNS s0 OBJCT 0.0000 C1 1.0000 s0 C13 1.0000 C20 1.0000 s0 C26 1.0000 C27 1.0000 s0 C28 1.0000 C29 1.0000 s0 C30 1.0000 C31 1.0000 s0 C47 1.0000 C48 1.0000 s0 C49 1.0000 C50 1.0000 s0 C51 1.0000 C52 1.0000 s1 OBJCT 1.0000 C1 -1.0000 s1 C2 1.0000 C14 -1.0000 s1 C21 1.0000 C32 1.0000 s1 C33 1.0000 C34 1.0000 s1 C35 1.0000 C36 1.0000 s1 C53 1.0000 C54 1.0000 s1 C55 1.0000 C56 1.0000 s1 C57 1.0000 s2 OBJCT 1.0000 C2 -1.0000 s2 C3 1.0000 C15 -1.0000 s2 C22 1.0000 C37 1.0000 s2 C38 1.0000 C39 1.0000 s2 C40 1.0000 C58 1.0000 s2 C59 1.0000 C60 1.0000 s2 C61 1.0000 s3 OBJCT 3.0000 C3 -1.0000 s3 C4 1.0000 C16 -1.0000 s3 C23 1.0000 C41 1.0000 s3 C42 1.0000 C43 1.0000 s3 C62 1.0000 C63 1.0000 s3 C64 1.0000 s4 OBJCT 1.0000 C4 -1.0000 s4 C5 1.0000 C17 -1.0000 s4 C24 1.0000 C44 1.0000 s4 C45 1.0000 C65 1.0000 s4 C66 1.0000 s5 OBJCT 1.0000 C5 -1.0000 s5 C6 1.0000 C18 -1.0000 s5 C25 1.0000 C46 1.0000 s5 C67 1.0000 s6 OBJCT 2.0000 C6 -1.0000 s6 C19 -1.0000 x1 OBJCT 0.0000 C1 1.0000 x1 C7 1.0000 C14 1.0000 x2 OBJCT 0.0000 C2 1.0000 x2 C8 1.0000 C15 1.0000 x3 OBJCT 0.0000 C3 1.0000 x3 C9 1.0000 C16 1.0000 x4 OBJCT 0.0000 C4 1.0000 x4 C10 1.0000 C17 1.0000 x5 OBJCT 0.0000 C5 1.0000 x5 C11 1.0000 C18 1.0000 x6 OBJCT 0.0000 C6 1.0000 x6 C12 1.0000 C19 1.0000 MARK0001 'MARKER' 'INTORG' y1 OBJCT 8.0000 C7 -34.0000 y1 C14 -6.0000 C20 6.0000 y1 C26 6.0000 C27 13.0000 y1 C28 17.0000 C29 23.0000 y1 C30 26.0000 C31 34.0000 y1 C47 6.0000 C48 13.0000 y1 C49 17.0000 C50 23.0000 y1 C51 26.0000 C52 34.0000 y2 OBJCT 12.0000 C8 -34.0000 y2 C15 -7.0000 C21 7.0000 y2 C27 13.0000 C28 17.0000 y2 C29 23.0000 C30 26.0000 y2 C31 34.0000 C32 7.0000 y2 C33 11.0000 C34 17.0000 y2 C35 20.0000 C36 28.0000 y2 C48 13.0000 C49 17.0000 y2 C50 23.0000 C51 26.0000 y2 C52 34.0000 C53 7.0000 y2 C54 11.0000 C55 17.0000 y2 C56 20.0000 C57 28.0000 y3 OBJCT 8.0000 C9 -34.0000 y3 C16 -4.0000 C22 4.0000 y3 C28 17.0000 C29 23.0000 y3 C30 26.0000 C31 34.0000 y3 C33 11.0000 C34 17.0000 y3 C35 20.0000 C36 28.0000 y3 C37 4.0000 C38 10.0000 y3 C39 13.0000 C40 21.0000 y3 C49 17.0000 C50 23.0000 y3 C51 26.0000 C52 34.0000 y3 C54 11.0000 C55 17.0000 y3 C56 20.0000 C57 28.0000 y3 C58 4.0000 C59 10.0000 y3 C60 13.0000 C61 21.0000 y4 OBJCT 6.0000 C10 -34.0000 y4 C17 -6.0000 C23 6.0000 y4 C29 23.0000 C30 26.0000 y4 C31 34.0000 C34 17.0000 y4 C35 20.0000 C36 28.0000 y4 C38 10.0000 C39 13.0000 y4 C40 21.0000 C41 6.0000 y4 C42 9.0000 C43 17.0000 y4 C50 23.0000 C51 26.0000 y4 C52 34.0000 C55 17.0000 y4 C56 20.0000 C57 28.0000 y4 C59 10.0000 C60 13.0000 y4 C61 21.0000 C62 6.0000 y4 C63 9.0000 C64 17.0000 y5 OBJCT 10.0000 C11 -34.0000 y5 C18 -3.0000 C24 3.0000 y5 C30 26.0000 C31 34.0000 y5 C35 20.0000 C36 28.0000 y5 C39 13.0000 C40 21.0000 y5 C42 9.0000 C43 17.0000 y5 C44 3.0000 C45 11.0000 y5 C51 26.0000 C52 34.0000 y5 C56 20.0000 C57 28.0000 y5 C60 13.0000 C61 21.0000 y5 C63 9.0000 C64 17.0000 y5 C65 3.0000 C66 11.0000 y6 OBJCT 23.0000 C12 -34.0000 y6 C19 -8.0000 C25 8.0000 y6 C31 34.0000 C36 28.0000 y6 C40 21.0000 C43 17.0000 y6 C45 11.0000 C46 8.0000 y6 C52 34.0000 C57 28.0000 y6 C61 21.0000 C64 17.0000 y6 C66 11.0000 C67 8.0000 RHS RHS1 C1 6.0000 C2 7.0000 RHS1 C3 4.0000 C4 6.0000 RHS1 C5 3.0000 C6 8.0000 RHS1 C20 6.0000 C21 7.0000 RHS1 C22 4.0000 C23 6.0000 RHS1 C24 3.0000 C25 8.0000 RHS1 C26 6.0000 C27 13.0000 RHS1 C28 17.0000 C29 23.0000 RHS1 C30 26.0000 C31 34.0000 RHS1 C32 7.0000 C33 11.0000 RHS1 C34 17.0000 C35 20.0000 RHS1 C36 28.0000 C37 4.0000 RHS1 C38 10.0000 C39 13.0000 RHS1 C40 21.0000 C41 6.0000 RHS1 C42 9.0000 C43 17.0000 RHS1 C44 3.0000 C45 11.0000 RHS1 C46 8.0000 C47 6.0000 RHS1 C48 13.0000 C49 17.0000 RHS1 C50 23.0000 C51 26.0000 RHS1 C52 34.0000 C53 7.0000 RHS1 C54 11.0000 C55 17.0000 RHS1 C56 20.0000 C57 28.0000 RHS1 C58 4.0000 C59 10.0000 RHS1 C60 13.0000 C61 21.0000 RHS1 C62 6.0000 C63 9.0000 RHS1 C64 17.0000 C65 3.0000 RHS1 C66 11.0000 C67 8.0000 BOUNDS FR BND s0 FR BND s1 FR BND s2 FR BND s3 FR BND s4 FR BND s5 FR BND s6 FR BND x1 FR BND x2 FR BND x3 FR BND x4 FR BND x5 FR BND x6 UP BND y1 1 UP BND y2 1 UP BND y3 1 UP BND y4 1 UP BND y5 1 UP BND y6 1 ENDATA
附录3 整数规划解
+Leapms>mip relexed_solution=44.8078; number_of_nodes_branched=0; memindex=(1,2) The Problem is solved to optimal as an MIP. 找到整数规划的最优解.非零变量值和最优目标值如下: ......... s1* =11 s2* =4 s5* =8 x1* =17 x4* =6 x5* =11 y1* =1 y4* =1 y5* =1 ......... Objective*=47 ......... +Leapms>
参考文献
[1] Wolsey L A. Integer Programming. New York: Jonh Wiley & Sons, 1998 / ISBN 978-0-471-28366-9
[2] Barany I. Strong Formulations for Multi-Item Capacitated Lot Sizing[J]. Management Science, 1984, 30(30):1255-1261.
[3] Wolsey L A. Uncapacitated Lot-Sizing Problems with Start-Up Costs[J]. Operations Research, 1989, 37(5):741-747.
[4] Belvaux G, Wolsey L A. bc-prod: A Specialized Branch-and-Cut System for Lot-Sizing Problems[J]. Management Science, 2000, 46(5):724-738.
[5] Wolsey L A. Erratum: A tight formulation for uncapacitated lot-sizing with stock upper bounds[J]. Mathematical Programming, 2017, 161(1-2):1-7.