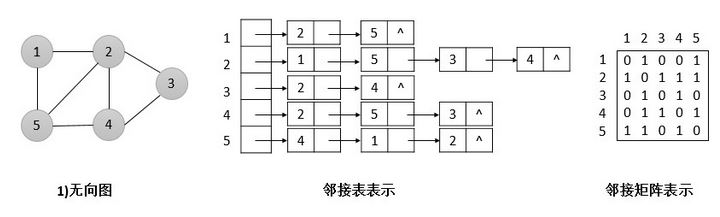
首先我们先说下图论,一般图存储可以使用邻接矩阵,或邻接表,一般使用邻接矩阵在稠密图比较省空间。
我们来说下有向图,一般的有向图也是图,图可以分为稠密图,稀疏图,那么从意思上,稠密图就是点的边比较多,稀疏图就是边比较少的图。为什么稠密图放在矩阵比较省空间,因为邻接表在边之间存储需要多余的指针,而矩阵不需要。
下面这张图:http://blog.csdn.net/tham_/article/details/46048063
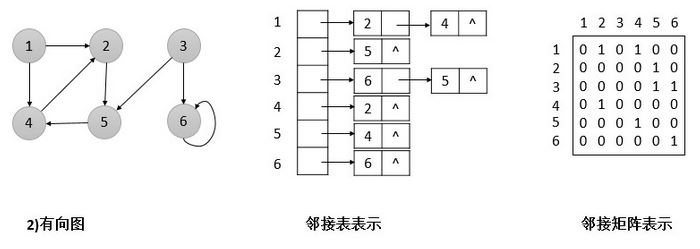
我们只说有向图,我们把有向图存在矩阵
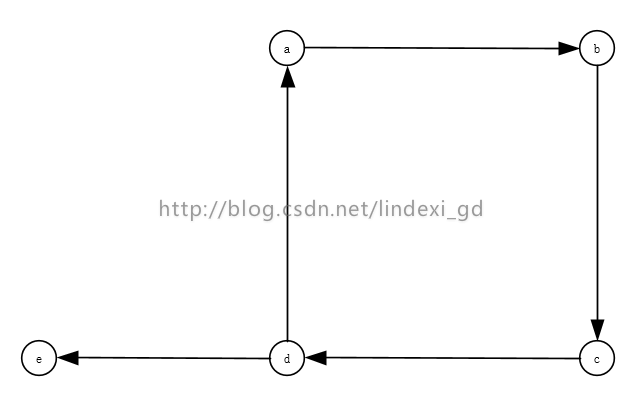
我们先说Warshall,假如我们有一张图
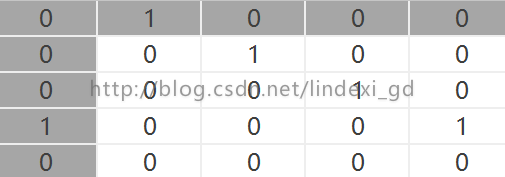
我们把这张图存储在矩阵
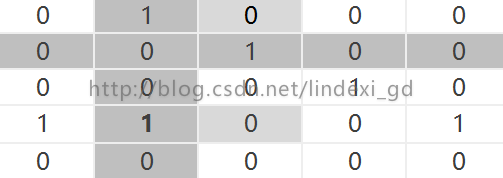
首先是a,a可以直接到b,那么ab就是1
接着就是b,b可以直接到c,那么bc就是1
| Warshall | a | b | c | d | e |
|---|---|---|---|---|---|
| a | 0 | 1 | 0 | 0 | 0 |
| b | 0 | 0 | 1 | 0 | 0 |
| c | 0 | 0 | 0 | 1 | 0 |
| d | 1 | 0 | 0 | 0 | 1 |
| e | 0 | 0 | 0 | 0 | 0 |
那么Warshall怎么做,他需要做个十字形,因为有个定理,
其中ijk都是从0到n,这里n是点个数
那么我们得到的第一个矩阵,叫做
那么由第一个矩阵变化出第二个矩阵就叫
然后一直到n,这里n是点个数
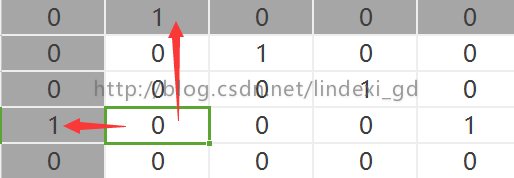
如何变化,其实很简单,做个十字,这里说的十字是
那么我们第一个公式就可以来
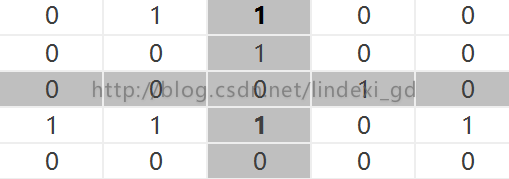
我们选择一个点
如果在十字两个都是1,那么这个点也就改为1,因为图里只有一个点可以修改,所以修改完就是
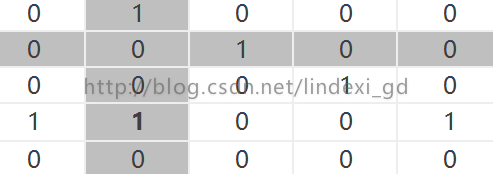
接着我们把十字修改
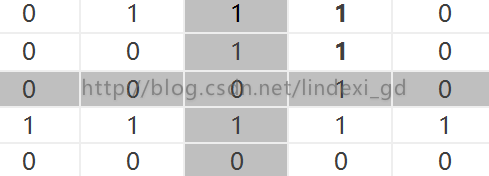
那么发现有两个点,加粗db是上次修改的
我们可以发现ac和dc都是可以修改
那么继续修改
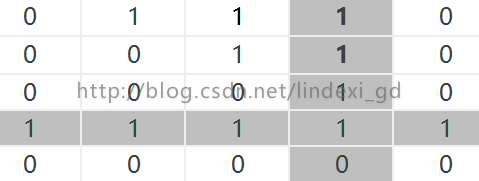
修改后
| Warshall | a | b | c | d | e |
|---|---|---|---|---|---|
| a | 1 | 1 | 1 | 1 | 1 |
| b | 1 | 1 | 1 | 1 | 1 |
| c | 1 | 1 | 1 | 1 | 1 |
| d | 1 | 1 | 1 | 1 | 1 |
| e | 0 | 0 | 0 | 0 | 0 |
因为我们从a到d都是可以到达,所以都为1,因为存在d可以到e,所以所有点都可以到e,因为e本身没有到任何点,所以为0
那么Floyd是什么,其实就是把原先的矩阵1改为数字
Floyd是可以算图中任意两个点的最短路径
那么说道这,我们需要带权有向图
带权就是两个点之间的边有个权,放在矩阵就是可以相连的两个点之间的ij为权
1
| Warshall | a | b | c | d | e |
|---|---|---|---|---|---|
| a | 0 | 5 | |||
| b | 0 | 2 | |||
| c | 0 | 1 | |||
| d | 6 | 15 | 0 | 1 | |
| e | 0 |
我们和之前Warshall一样做十字,然后判断是得到
那么这样就可以得到任意两点路径
算法复杂
在Warshall是判断两个都为1,修改,Floyd判断两个加起来的值比当前的小,修改
和Warshall一样全部修改就是两个点之间最短距离。
为
任意一个数字小于