力扣51题（n皇后）

51.N皇后

基本思想：

回溯算法

具体实现：

力扣题解抄的

1、在N皇后问题中，这颗决策树的每一行节点对应棋盘上的行，每行节点中的节点位置对应棋盘上的列，这样可以构建出一颗决策树。此时，回溯法求解N皇后问题，就变成求解决策树中所有可能的从根节点到叶节点的路径。需要注意的是，N皇后问题中各皇后不能冲突，因此在遍历树的路径时，设定一些条件即可：

2、皇后不能在同一行：backtrack函数中，依次从上到下处理不同的行，即可满足这一条件；

皇后不能在同一列：用col_selected列表记录曾经选择过的列，下次选择时，如果要选择的列没有被选择过，才可以加入路径；

皇后所在的主对角线上不能有其他皇后：若令其行和列的索引分别为i和j，则同一主对角线上元素的行列索引之差等于同一常数i-j；

皇后所在的次对角线上不能有其他皇后：若令其行和列的索引分别为i和j，则同一次对角线上元素的行列索引之和等于同一常数i+j；

j not in col_selected and (i-j not in z_diag )and (i+j not in f_diag):

3、set（）函数

 代码：

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        # 回溯法
        res = []
        s = '.' * n
        def backtrack(path=[], i=0, col_selected=[], z_diag=set(), f_diag=set()):
            if i == n:
                res.append(path)
                return 
            for j in range(n):
                if j not in col_selected and i-j not in z_diag and i+j not in f_diag:
                    backtrack(path+[s[:j]+'Q'+s[j+1:]], i+1, col_selected+[j], z_diag|{i-j}, f_diag|{i+j})
            
        backtrack()
        return res

基本思想：

代码随想录抄的

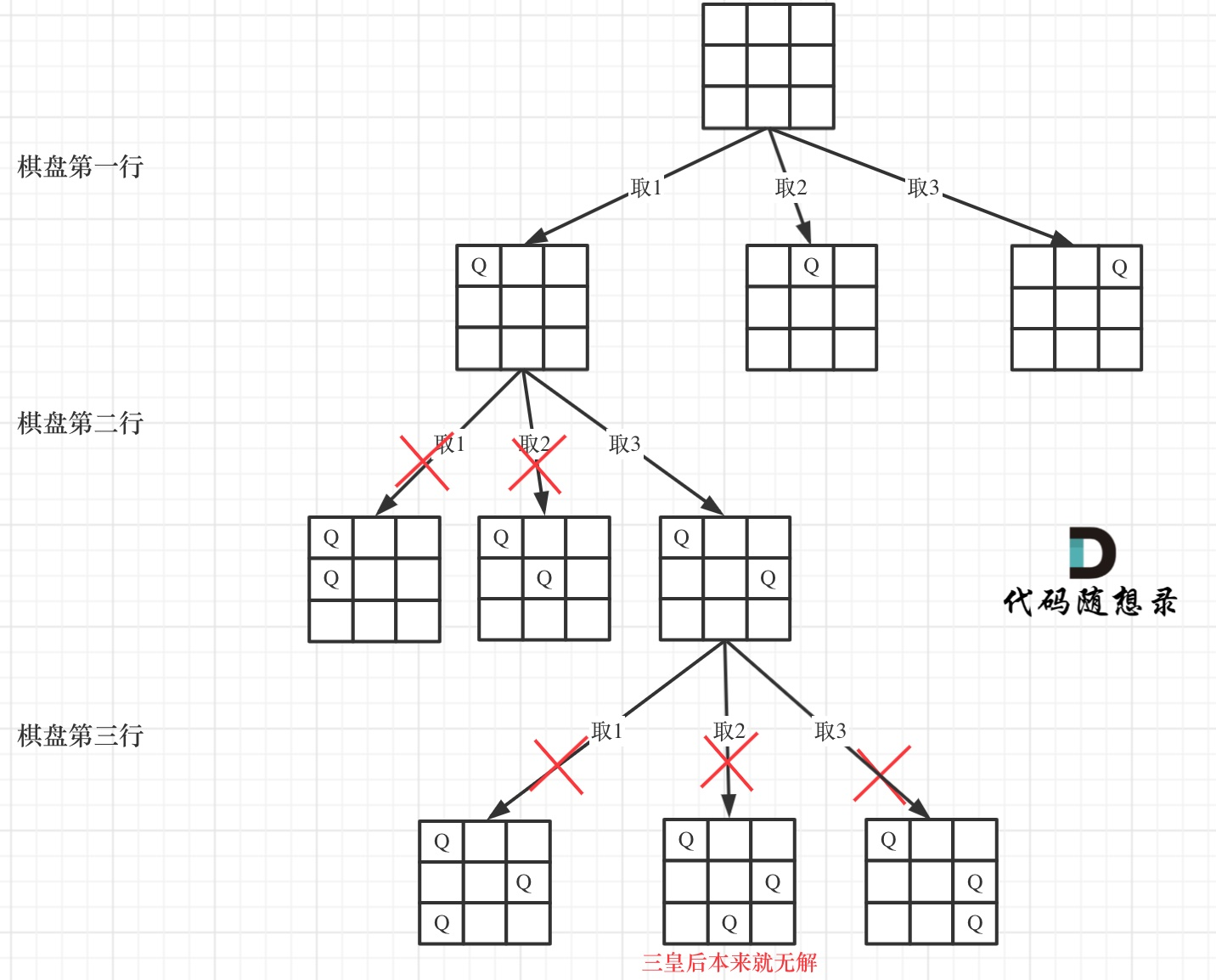
递归深度就是row控制棋盘的⾏，也就是二维矩阵的高

每⼀层⾥for循环的col控制棋盘的列，⼀⾏⼀列，确定了放置皇后的位置

1.递归参数：二维数组result，棋盘大小n，记录遍历到第几层的row

2.递归终止条件：row == n

if (row == n) {
    result.push_back(chessboard);
    return;
}

3.单层搜索逻辑：

每次都要从新的一行的起始位置开始搜，所以col都是从0开始

for (int col = 0; col < n; col++) {
    if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
        chessboard[row][col] = 'Q'; // 放置皇后
        backtracking(n, row + 1, chessboard);
        chessboard[row][col] = '.'; // 回溯，撤销皇后
    }
}

4.验证棋牌是否合法

不需要再代码中检查，是否同行

因为在单层搜索的过程中，每一层递归，只会选for循环（也就是同一行）里的一个元素，所以不用去重了。

代码：

class Solution {
    List<List<String>> res = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        char[][] chessboard = new char[n][n];
        for (char[] c : chessboard) {
            Arrays.fill(c, '.');
        }
        backTrack(n, 0, chessboard);
        return res;
    }


    public void backTrack(int n, int row, char[][] chessboard) {
        if (row == n) {
            res.add(Array2List(chessboard));
            return;
        }

        for (int col = 0;col < n; ++col) {
            if (isValid (row, col, n, chessboard)) {
                chessboard[row][col] = 'Q';
                backTrack(n, row+1, chessboard);
                chessboard[row][col] = '.';
            }
        }

    }


    public List Array2List(char[][] chessboard) {
        List<String> list = new ArrayList<>();

        for (char[] c : chessboard) {
            list.add(String.copyValueOf(c));
        }
        return list;
    }


    public boolean isValid(int row, int col, int n, char[][] chessboard) {
        // 检查列
        for (int i=0; i<row; ++i) { // 相当于剪枝
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }

        // 检查45度对角线
        for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }

        // 检查135度对角线
        for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }
}