我们是通过算法来找到数据之间的关联规则(两个物品之间可能存在很强的相关关系)和频繁项集(经常出现在一起的物品的集合)。
我们是通过支持度和置信度来定义关联规则和频繁项集的
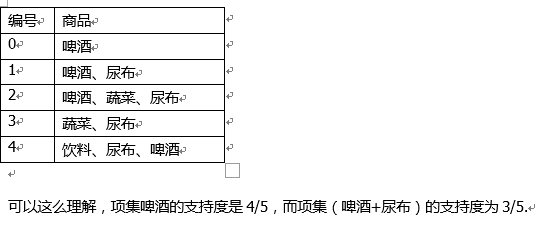
一个项集支持度是指在所有数据集中出现这个项集的概率,项集可能只包含一个选项,也有可能是多个选项的组合。
置信度 针对于啤酒——>尿布这样的关联规则来定义,计算方式为支持度(啤酒,尿布)/支持度啤酒,其中支持度(啤酒、尿布)为3/5,支持度啤酒为4/5,所以他的置信度为3/4,即置信度为75%,这意味着在啤酒的规则中,有0.75的规则都适用。
但是在这样的规则中,如果需要求出所有规则,那么计算量比较大,这就可以用到 Apriori算法
Apriori 的原理:如果某个项集是频繁项集,那么它所有的非空子集也是频繁的(先验原理)。即如果 {0,1} 是频繁的,那么 {0}, {1} 也一定是频繁的。反过来能发现如果一个项集是非频繁的,那么它的所有超集也是非频繁的。这样就不用计算他的支持度了,可以减少计算量。
计算步骤为:
先会生成所有单个物品的项集列表, 扫描交易记录来查看哪些项集满足最小支持度要求(一般会给一个最小支持度),那些不满足最小支持度的集合会被去掉,对剩下的集合进行组合以生成包含两个元素的项集,接下来重新扫描交易记录,去掉不满足最小支持度的项集,重复进行直到所有项集都被去掉。
提高Apriori算法的效率
1、基于散列的技术
当扫描数据库中的每个事务时,由C1中的候选频繁项集1项集产生频繁项集1项集L1时,可以对每个事务产生所有的2项集,将他们散列(映射)到散列表中的不同桶中,并增加对应的桶计数。在散列表中,对应桶计数低于支持度阈值的2项集不可能是频繁的,可以删除掉。
2、事物压缩
不包含任何频繁项集的K项集的事务不可能包含任何频繁(K+1)项集。这种事务在之后的考虑时,可以被标记或者删除,因为产生的j项集(j>K) 的数据库扫描不再需要他们。
3、划分
包含两个阶段,第一阶段,算法把D中的事务分成n个非重叠的分区,如果D中事务的最小相对支持度阈值为p,则每个分区的最小支持度为p乘该分区中的事务数。对每个分区,找到所有的局部频繁项集。 阶段二是,再次扫描D,评估每个候选的实际支持度,以确定全局频繁项集。
4、抽样
选取给你定数据库D中的随机样本S,然后在S而不再D中搜索频繁项集。
5、动态项集技术