上一课了解了栈这种线性结构,这节学另一种线性结构——队列。队列这个名字相比栈好理解些,这个名字源自排队买票,先来的人先买后来的后买,所以它的特点和栈正好相反,是先进先出后进后出

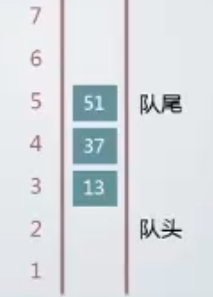
在栈里面有栈顶栈底的概念,在队列里面有类似的概念,我们称为队头队尾。栈是一端开口一端封口,队列是两端都是开口的。当我们刚开始排队时先站在队尾,然后从对头离队,所以队列的特点是从队尾入队然后从队头出队。
通常我们也是使用队头队尾这两个指针来共同指向一个数组,入队时队尾指针向后移动一位,出队是队头指针也向后移动一位,所以在队列里面队头和队尾这两个指针都是可以移动的,因此我们使用队列时必须把这两个指针结合在一起来判断这个队列现在属于什么状态。

所以现在我们知道了,入队时队尾指针向后移动一位,出队的时候队头指针往后移动一位,但是这样以来就有了一个很大的问题,如果说我们用数组来存储队列的话,无论是出队还是入队两个指针都是只往后移动不往前移动的,所以随着出队次数的变多,队头指针指针就会不断的往后移。比如一个数组它的上限是十,刚开始的时候队头指针还是好好的都是指向0这个位置的,但是随着一次次的入队出队入队出队,现在队头指针已经指向5了,这意味着从0到4这几个元素位置就空出来了,这样以来显然造成了空间的浪费。而栈是没有这个问题的,因为栈底指针永远不变,但是队列因为队头指针要往后面移动,所以每出队一次队列的容量就少了一个,这样下去显然是不行的。所以为了解决这个问题我们在队列的基础之上做改进,这种改进之后的队列叫做循环队列




所谓循环队列并不是什么新鲜的概念,它其实还是一种队列,只不过加了一个功能——当队尾或者队头的指针已经移动到了数组的上线,比如说数组的上线是10,现在队尾已经指到10了,现在我们还要入队,这时前面的0~4都是空着的,这个时候怎么办呢?就让队尾指针移动到0,我们假设0和10这边是连在一起的,所以这样对尾指针就跑到了队头指针的前面形成了一个环状,从头开始继续往后移动,这样做目的只有一个,就是把队头出队完浪费的这部分空间,让队尾给它循环利用起来,所以这样以来整个队列就形成了一个循环,所以就称为循环队列。
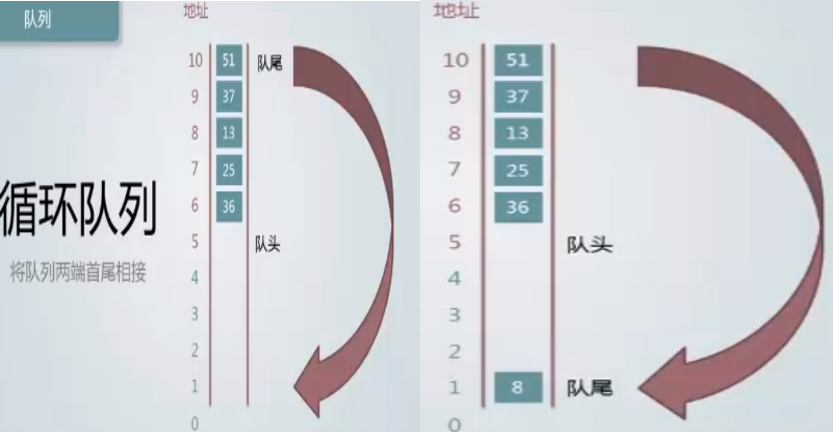
在讲循环队列以前知道队尾指针一定是在队头指针后面的,就好像栈里面栈顶指针一定是在栈底指针上面的,但是在引入了循环队列这个概念之后,发现循环队列里面的队尾指针有可能出现在队头指针前面的,所以提到循环队列的时候一定要记住:队头指针和队尾指针在循环队列里面是没有必然的大小关系的,这样以来给我们计算队列中元素的个数带来了一点麻烦

原本队尾肯定在队头的后面,所以如果队尾是5队头是3,直接一减就是2个元素。但是现在可能出现反过来的情况,可能队尾是3队头是5,这个时候就不能直接减了,要队尾-队头之后加上队列的容量


这种计算方法也是基于这节课所定义的这种队列形式来计算的,真正在考试时遇到的题目也要针对题目所定义的队列形式再来做具体的分析。最后再补充一点循环队列这种结构是为了弥补数组这种顺序存储结构的缺陷而产生的,如果我们采用链式存储结构来表示队列的话,它就不存在一个上限的问题,我们也就没有必要使用循环队列这种结构了,所以一提到循环队列它首先一定是一个顺序存储结构,当然如果我们使用链式存储结构的话因为它的地址不连续,我们也就不能像这节课这样直接拿地址相减了。