跳跃表SkipList的理解

     SkipList在各种开源引擎中用处普遍，例如redis的sortedset容器、luence里面的索引字典等均用到了skiplist。
1. SkipList
       在数据结构里面，我们知道有两种基本数据逻辑结构：数组和链表。它们均有其各自的特点，数组(特别是有序数组)，可以进行快速查询，但不便于删除操作;链表，可以进行快速的增删操作，但是又不便于查询。那有没可能存在一种数据结构，结合两者各自的优点呢？
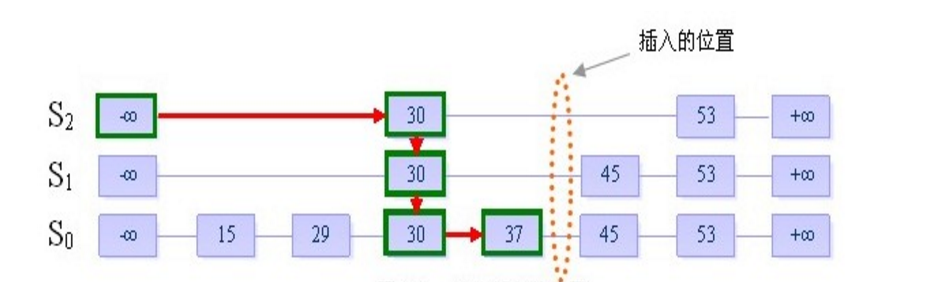
       基于这样的思路，William Pugh这位马里兰大学的计算机教授，于1989年提出来一种新的数据结构，跳跃表。其类似平衡二叉树的链表，但与排序二叉树相比的区别是，其兄弟相邻间的节点间用指针相连的。例如如下样例：

 1.1. 特征

   a. 从纵向角度看：
      它类似一种B+树，每一层均是其相邻低一层的子集。但与B+树相比的区别是，每一层的相邻节点间均是以指针相连。如果把它看成一种树，就会有相应的树高(height)。
   b. 从横向角度看：
      它是一种链表。越位于高层的链表，其元素越稀疏。每更高一层链表元素均是其相邻低一层的子集，那么其占相邻下一层的比例的多少，即是其跳跃的步数或间隔interval。

2. 读操作
       读取操作相对简单: 从最高层开始，优先横向游走，然后纵向游走，直到遇到目标元素。从跳跃标的特点可以看出，查找新元素的特点：
   a. 如果待查询值在跳跃表中，那么总是会在最底层的元素里；
   b. 从任意一层节点开始查询，均是可以找到结果的。
    源码如下：

statusEnum find(keyType key, recType *rec) {
  int i;
  nodeType *x = list.hdr;

  /*******************************
   *  find node containing data  *
   *******************************/

  for (i = list.listLevel; i >= 0; i--) {
    while (x->forward[i] != NIL && compLT(x->forward[i]->key, key))
      x = x->forward[i];
  }
  x = x->forward[0];
  if (x != NIL && compEQ(x->key, key)) {
    *rec = x->rec;
    return STATUS_OK;
  }
  return STATUS_KEY_NOT_FOUND;
}

3. 写操作

      在插入一个新的元素时，通常我们需要敲定2个问题，确定横向所在的位置与纵向所在的位置。如上图，如果现需要插入一个值为40的元素。
 a. 横向位置
     由于每一层链表均是有序的，所以对于一个给定的新元素，其横向位置基本通过查询操作可以快速确定和唯一的。
 b. 纵向位置
     根据跳跃表的定义，我们从上图可以看出，新元素40放入的层高可以位于0至4层之间的任意一层的。但是其放在的层高即纵向位置又是能直接决定了其纵向的树高(height)与每层横向跳跃的平均间隔(interval)的，因此得考虑其纵向位置的合理性。
     如果按照二叉的思路构建跳跃表的话，可以想象：100%的元素位于0层，50%的元素位于1层，25%的元素位于2层，以此类推。。所以，写入新的元素的规则，尽量保持跳跃表各层次类似二叉树的“身材”，避免各层次的变形，因此在放入新的元素时，通常按二叉树各层次元素个数来计算相应的概率，进行层数的敲定：

protected int ChooseRandomHeight()
{
  static const double _prob = 0.5;
  int level = 0;
  while ( _rndNum.NextDouble() < _prob )
  {
   level++;
  }
  return level;
} 

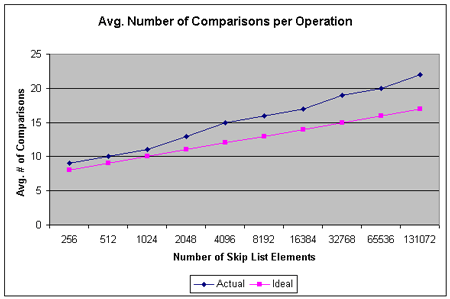
4. 效率

      在"probabilistic analysis of skip lists"文中分析了skiplist的增删操作平均运行时间是log2n, 在最坏情况下运行时间是线性的时间，当然这种最坏的情况发生的概率非常小。                                                               

5. 源码

/* skip list */
#include <stdio.h>
#include <stdlib.h>

/* implementation dependent declarations */
typedef enum {
  STATUS_OK,
  STATUS_MEM_EXHAUSTED,
  STATUS_DUPLICATE_KEY,
  STATUS_KEY_NOT_FOUND
} statusEnum;

typedef int keyType;            /* type of key */

/* user data stored in tree */
typedef struct {
  int stuff;                  /* optional related data */
} recType;

#define compLT(a,b) (a < b)
#define compEQ(a,b) (a == b)

/* levels range from (0 .. MAXLEVEL) */
#define MAXLEVEL 15

typedef struct nodeTag {
  keyType key;                /* key used for searching */
  recType rec;                /* user data */
  struct nodeTag *forward[1]; /* skip list forward pointer */
} nodeType;

/* implementation independent declarations */
typedef struct {
  nodeType *hdr;              /* list Header */
  int listLevel;              /* current level of list */
} SkipList;

SkipList list;                  /* skip list information */

#define NIL list.hdr

statusEnum insert(keyType key, recType *rec)
{
  int i, newLevel;
  nodeType *update[MAXLEVEL+1];
  nodeType *x;

  /***********************************************
   *  allocate node for data and insert in list  *
   ***********************************************/

  /* find where key belongs */
  x = list.hdr;
  for (i = list.listLevel; i >= 0; i--) {
    while (x->forward[i] != NIL && compLT(x->forward[i]->key, key))
      x = x->forward[i];
    update[i] = x;
  }
  x = x->forward[0];
  if (x != NIL && compEQ(x->key, key))
    return STATUS_DUPLICATE_KEY;

  /* determine level */
  for (
           newLevel = 0;
           rand() < RAND_MAX/2 && newLevel < MAXLEVEL;
           newLevel++);

  if (newLevel > list.listLevel) {
    for (i = list.listLevel + 1; i <= newLevel; i++)
      update[i] = NIL;
    list.listLevel = newLevel;
  }

  /* make new node */
  if ((x = static_cast<nodeType*>(malloc(sizeof(nodeType) + newLevel*sizeof(nodeType *)))) == 0)
    return STATUS_MEM_EXHAUSTED;
  x->key = key;
  x->rec = *rec;

  /* update forward links */
  for (i = 0; i <= newLevel; i++) {
    x->forward[i] = update[i]->forward[i];
    update[i]->forward[i] = x;
  }
  return STATUS_OK;
}

statusEnum free(keyType key) {
  int i;
  nodeType *update[MAXLEVEL+1], *x;

  /*******************************************
   *  delete node containing data from list  *
   *******************************************/

  /* find where data belongs */
  x = list.hdr;
  for (i = list.listLevel; i >= 0; i--) {
    while (x->forward[i] != NIL && compLT(x->forward[i]->key, key))
      x = x->forward[i];
    update[i] = x;
  }
  x = x->forward[0];
  if (x == NIL || !compEQ(x->key, key)) return STATUS_KEY_NOT_FOUND;

  /* adjust forward pointers */
  for (i = 0; i <= list.listLevel; i++) {
    if (update[i]->forward[i] != x) break;
    update[i]->forward[i] = x->forward[i];
  }

  free (x);

  /* adjust header level */
  while ((list.listLevel > 0)
         && (list.hdr->forward[list.listLevel] == NIL))
    list.listLevel--;

  return STATUS_OK;
}

statusEnum find(keyType key, recType *rec) {
  int i;
  nodeType *x = list.hdr;

  /*******************************
   *  find node containing data  *
   *******************************/

  for (i = list.listLevel; i >= 0; i--) {
    while (x->forward[i] != NIL && compLT(x->forward[i]->key, key))
      x = x->forward[i];
  }
  x = x->forward[0];
  if (x != NIL && compEQ(x->key, key)) {
    *rec = x->rec;
    return STATUS_OK;
  }
  return STATUS_KEY_NOT_FOUND;
}

void initList() {
  int i;

  /**************************
   *  initialize skip list  *
   **************************/

  if ((list.hdr = static_cast<nodeType*>(malloc(
          sizeof(nodeType) + MAXLEVEL*sizeof(nodeType *)))) == 0) {
    printf ("insufficient memory (initList)
");
    exit(1);
  }
  for (i = 0; i <= MAXLEVEL; i++)
    list.hdr->forward[i] = NIL;
  list.listLevel = 0;
}

int main(int argc, char **argv) {
  int i, maxnum, random;
  recType *rec;
  keyType *key;
  statusEnum status;


  /* command-line:
   *
   *   skl maxnum [random]
   *
   *   skl 2000
   *       process 2000 sequential records
   *   skl 4000 r
   *       process 4000 random records
   *
   */

  maxnum = 1000;//atoi(1000);
  random = 10;

  initList();

  if ((rec = static_cast<recType*>(malloc(maxnum * sizeof(recType)))) == 0) {
    fprintf (stderr, "insufficient memory (rec)
");
    exit(1);
  }
  if ((key = static_cast<keyType*>(malloc(maxnum * sizeof(keyType)))) == 0) {
    fprintf (stderr, "insufficient memory (key)
");
    exit(1);
  }

  if (random) {
    /* fill "a" with unique random numbers */
    for (i = 0; i < maxnum; i++) key[i] = rand();
    printf ("ran, %d items
", maxnum);
  } else {
    for (i = 0; i < maxnum; i++) key[i] = i;
    printf ("seq, %d items
", maxnum);
  }

  for (i = 0; i < maxnum; i++) {
    status = insert(key[i], &rec[i]);
    if (status) printf("pt1: error = %d
", status);
  }

  for (i = maxnum-1; i >= 0; i--) {
    status = find(key[i], &rec[i]);
    if (status) printf("pt2: error = %d
", status);
  }

  for (i = maxnum-1; i >= 0; i--) {
    status = free(key[i]);
    if (status) printf("pt3: error = %d
", status);
  }
  return 0;
}

参考：

   1. "Skip Lists: A Probabilistic Alternative to Balanced Trees"
   2. "Probabilistic Analysis of Skip Lists"
   3. https://msdn.microsoft.com/en-us/library/ms379573(v=vs.80).aspx
   4. http://www.cppblog.com/mysileng/archive/2013/04/06/199159.html