持续掉线……重连中……[fail:因为太菜]……
容斥原理
好吧其实它就是长这样的东西的变种
然后我们用它来计算一下欧拉函数公式
众所周知,欧拉函数就是1~n中与n互质的数
如果(n = p_1 ^ {r_1} * p_2^{r_2}……*p_m^{r_m})
那么补集转换一波,欧拉函数可以看作(n - |p_1的倍数 cup p_2的倍数 cup ……cup p_m的倍数|)
看到这个东西 我们觉得十分熟悉,就把它变成
(sum_{T in [n]} (-1)^T |cap_{i in T} S_i|)
因为(|cap_{i in T} S_i| = frac{n}{prod_{i in T}p_i})
所以原式$ = sum_{T in [n]} (-1)^T frac{n}{prod_{i in T}p_i}$
又因为(prod_{i = 1}^{n} (1 + x_i) = sum_{S in [n]}(prod_{i in S} x_i))
所以原式 (= sum_{T in [n]} (-1)^T frac{n}{prod_{i in T}p_i})
$ = n sum_{T in [n]} (-1)^T frac{1}{prod_{i in T}p_i}$
$ = nprod_{i = 1}^{m} (1 - frac{1}{p_i})$
-
已知(x_1 + x_2 + …… + x_n = A, 0 leq x_i leq C_i)
求有多少组解
如果是问(p leq x_i)的话就很好办 先强行去掉p就好了
比如要求(1 leq x_1)其他(x_i)无限制的话
就相当于解所有(x_i)都无限制的(x_1 + x_2 + ... + x_n = A - 1)
然后把解得的(x_1)加上一就好了
所以这里 (0 leq x_i leq C_i)的解法就是
ans = 无限制解数 - 只限制(C_1 leq x_1)解数 - 只限制(C_2 leq x_2)解数 - ....... + 只限制(C_1 leq x_1)且(C_2 leq x_2)解数 + 只限制(C_2 leq x_2)且(C_3 leq x_3)解数 + .....
这样容斥下去就行了
-
有一个长度位为n - 1的由"<"和">"组成的序列
你需要计算使得 p[i]<p[i+1] 当且仅当 s[i] 为 < 的排列 p的数量
n<=10^5
如果这个序列里只有"<"就很好办 递增就好了嘛
考虑把所有">"变成无限制 得到的排列集合显然包含原来">"在时的排列
而这个集合里多出来的排列 就是该">"变成"<"后的合法排列
那么就可以容斥了
考虑若干个">"变成"<"合法数量
被变成无限制的">"就把原生的次生的"<"划分成了一些连续"<"区间
比如这个序列 < < ? ? < ? < 就被划分成A < B < C | D | E < F | G < H
每个区间里的元素是递增的(比如第一个区间里A < B < C)
所以这时排列的种类数就是(frac{n!}{len_1!len_2!...len_k!})(k是被划分成的区间数)
ans = 所有">"变成无限制合法数量 - 一个">"变成"<",其他">"变成无限制合法数量 + 两个">"变成"<",其他">"变成无限制合法数量 .....
然而(n leq 1e5) 事情就变得尴尬起来
考虑每一个">"变成"<"之后会对系数贡献-1 变成"="会贡献1(所谓贡献-1就是让系数乘上-1)
那么推一推就可以发现一件有趣的事情
(f[i] = sum f[j] frac{1}{(i - j)!} (-1)^{j + 1 -> i - 1位置之间的">"数量})(f[i]表示第i个">"之前的答案,也就是截至第k个区间)
最后答案就是(n! f[k])
p.s. dls说到了个很有趣的东西
随机1~n的排列的大小关系 和随机n个(0, 1)实数的大小关系是等价的
-
SetAndSet
有n个数,n<=50,要分成⾮空的两组,对每组把所有数and起来。要使得结果⼀样。⽐如{1,2,3,4},那么{1,2},{3,4}的分组是合法的,因为1 and 2 = 0 ,3 and 4 = 0。
每个数<=2^20。
补集转换。考虑怎么才能不一样呢?对于某一位,序列可以看作由0,1组成。
如果要不同的话 划分至少要在一位一侧有一,另一侧全是零
然而这个很好统计 并查集+搜索枚举就可以了
对于每一种情况的结果都是(2^{连通块个数} - 2)
- Min-Max容斥
(max(x_1, x_2, x_3, ... , x_n) = x_1 + x_2 + ... + x_n - min(x_1, x_2) - min(x_2, x _3) ...)
这个东西常常被用在期望的计算中
- 每次产⽣S的概率为p(S),并问全集的期望步数。 |U|<=20
一个集合被产生的期望步数,就是它里面最后一个元素被产生的期望步数
那么(E[max_{i = 1}^{n} x_i] = sum_{T subset [n],T eq emptyset}(-1)^{|T|}E[min_{i in T}x_i])
而T中第一个元素被选到的概率
就是T所有子集或者与T相交的集合中被选到一个的概率
但与T相交的集合非常不好算
所以把它变成选择不是上述以外其他集合的概率
也就是(1 - sum_{S subset UT}P(S))
期望步数就是(frac{1}{1 - sum_{S subset UT}P(S)})
补充一下集合前缀和的求法
for(int i = 0; i < n; ++i)
for(int S = 0; S <= (2 << n) - 1; ++S)
if(S & (1 << i)) f[S] += f[S - (1 << i)];
-
一个课件有n道题,每次再放送会以p概率讲到
求讲遍所有题的再放送期望次数
这道题和上一道极为类似
(ans = sum_{i = 1}^{n} (-1)^{i} binom{n}{i} frac{1}{1 - (1 - p)^i})
- 「PKUWC2018」随机游走
看到遍历..期望..就四舍五入是Min-Max啦
大致思路就是递推出每个点被走到的期望+Min-Max容斥
小菜鸡我比较感兴趣的是递推那部分
(以下式子建议手推一下,直接看不易理解)
快乐高消的时候我们有(f_u = 1+ frac{1}{d_u}(sum_{v in ch[d]}f_v + f_{fa}))
复杂度(O(2^n n^3))
强行(f_u = A_u f_{fa} + B_u)
则移项一下有((1 - frac{sum A_v}{d_u})f_u = frac{1}{d_u}f_{fa} + frac{1}{d_u}sum B_v + 1)
然后我们的叶子有(f_v = f_{fa} + 1) 有A,B,而根有f[root] = 0
所以从下向上收获一波A, B,再从上到下收获f[]就好啦
复杂度(O(2^n n))
- 有⼀个完全图每条边红⿊染⾊,求同⾊三⻆形个数。
这道题好妙啊,对于异色三角形,它有两个角是两边异色的
所以(sum_{i = 1}^{n} (i连的红边数) * (i连的黑边数))就是异色三角形数,用所有三角形数减一下就是答案了
- 插播:众所周知对于一个环上的n个点 随便钦点三条线段 它们会有如下五种关系
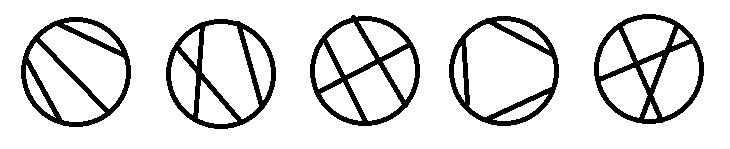
(设它们从左到右是A, B, C, D, E)
那么已知n((n leq 1e5)) 求D,E方案数之和
疯狂暗示这道题和上一道有某些联系
如果把线段当成点,相交的线段之间连红边,不相交的连蓝边 那么A, D, E就是同色三角形,又因为我们可以大力排列组合统计A,所以就能得到D,E了
据说数三角形可以树状数组二维数点?
- 连通图计数(有标号)
(f(n) = 2^{ binom{n}{2}} - sum_{i = 1}^{n - 1} binom{n - 1}{i - 1}f(i) 2^{ binom{n - i}{2}})
欧拉图计数(有标号)
$ f(n) = 2^{ binom{n - 1}{2} - sum_{i = 1}^{n - 1} binom{n - 1}{i - 1} f(i) 2^{ binom{n - i - 1}{2}}}$
首先对于连通图计数,用全集减去所有不连通的图
对于不连通的图,枚举1所在的连通块(即( binom{n - 1}{i - 1}f(i)))
其中f(i)表示大小为i的连通图有多少个
然后剩下的n - i个点不与这个块联通 随便连边就好了(即(2^{ binom{n - i}{2}}))
对于欧拉图计数,因为要求所有点度数为偶数,
所以可以看作构造好n-1个点的图后
(未必是连通图,而且对于任意一个图奇数度数点个数一定是偶数个)
点n向所有度数为奇数的点连边
所以类似于连通图 去掉不连通的欧拉图就好啦
- ([0, 2^n - 1])中选m个不同的数,使他们xor和为0的方案数(有序)
(ans = binom{2^n}{m - 1} - (m - 1)f[m - 2](2^n - m + 2))
其实这么写更容易理解
(f[m - 2](2^n - m + 2)(m - 1))
这三部分分别表示取了一个m-2的方案,此时还有((2^n - m + 2))个数可取
最后与倒数第二个数重复的第m个数可以放在任意位置(共m - 1个位置)
无序的话 除以(m!)就好了
-
bzoj2196
有N个点(编号1到N)组成的无向图,已经为你连了M条边。请你再连K条边,使得所有的点的度数都是偶数。求有多少种连的方法。要求你连的K条边中不能有重边,但和已经连好的边可以重。不允许自环的存在。求连边的方法数。
N≤1000,M≤N,K≤1000,K≤N(N-1)/2
(f[i][j])表示选了i条边,j个奇点
(f[i][j] = binom{j+2}{2}f[i - 1][j + 2] + (n - j) j f[i - 1][j] + binom{n - j + 2}{2}f[i - 1][j - 2] - (i - 1)( binom{n}{2} - (i - 2))f[i - 2][j])
最不好理解的就是((i - 1)( binom{n}{2} - (i - 2))f[i - 2][j])
它和上题一样 是故意取重边 其实这么写更容易理解
(f[i - 2][j]( binom{n}{2} - (i - 2))(i - 1))
这三部分分别表示取了一个i-2的方案,此时还有(( binom{n}{2} - (i - 2)))条边可取,当然这也是有序的
- 小星星
(link)[https://loj.ac/problem/2091]
p.s.这道题是周老师讲的啊,冤有头债有主啊
关于映射的定义,如果有蒟蒻如我不知道的话,题干里很贴心地hint了一下
“现在饰品中两颗小星星有细线相连,那么要求对应的小星星原来的图纸上也有细线相连。”
然后我们手玩一下。。。这是个乱七八糟的什么东西?怎么统计报警了?
众所周知,乱七八糟的东西用动态规划,不好统计的东西用容斥。
(f[T][i][j])表示以i为根的子树可以映射到图中,并且不映射到T中的点上
于是有转换(f[i][j] = sum_{p in ch[i],q in V[j]} f[p][q])
然后我们可以快乐容斥(sum_{T subset [n]} sum_{i in [n]T} (-1)^{|T|} f[T][root][i])
看起来很有道理是不是?
有锅都是周老师的就这样
- 凸包面积期望
之前敦爷讲过一个边在凸包上概率的计算(即所有点在它的一边
凸包面积等于凸包上相邻点的叉积和,那么枚举一条边两个点
求出这条边在凸包上的概率,再乘上两端点向量的叉积即可
如果有三点共线的话记得处理一下
-
Orienteering
⼀个n*m⽹格图,⾥⾯有⼀个四联通块构成了树,其他都是障碍。有不超过300个checkpoint。随机选取k个checkpoint,求通过这k个点最短路径的期望。
n,m<=50
这个树可以看作由|checkpoint|个点构成的边权为1的树
这条路径是由绕着轮廓线走一圈,去掉最远两点之间路径构成的
一条边对轮廓线贡献的期望是(因为长度为1所以数值上等于概率)
(2(frac{ binom{n}{k} - binom{size_l}{k} - binom{size_r}{k}}{ binom{n}{k}}))
(size_l)和(size_r)表示这条边左右所连子树的大小
然后考虑这条边对最远路径的贡献
如果(x, y)是最远路径 那么说明对于树上的任意一点i
满足(dis(x, i),dis(y, i) leq dis(x, y))
设对于(x, y)有t个这样的点 那么这条边的贡献期望就是(frac{ binom{t}{k - 2}}{ binom{n}{k}})
注意还会有最远路径重复的情况 这时让编号最小的点来做最远路径端点就好了
在选点的时候加一个判定即可
-
Company Acquisitions
有若⼲个公司,每个公司可能是根节点,也可能依附于某个根节点。 每次随机选两个根节点,然后让他们互怼。互怼失败的点归附胜者,它的儿子背离他而去成为独立的父节点。问期望多少步还剩⼀个节点。
似乎这是一道ppt朗读讲评题,那就直接贴ppt吧
假设每个东⻄对答案的贡献独⽴的,记c(x)表示有x个⼦公司对答案的贡献。
我们有(c(x)+c(y)=1+1/2(c(x+1)+y*c(0))+ 1/2(c(y+1)+x*c(0)))
可以分离变量得到$c(x)=1/2(c(x+1)+x*c(0)) $
边界: (c(n-1)=0)。然后进行一波大力递推。
-
Segment
有⼀个[1,n]的线段,每次随机选取⼀个中点,然后将其分成左右
两边[1,x],[x+1,n]递归下去,形成⼀个线段树的结构。
q个询问,每次问区间[l,r]在线段树中期望会访问⼏个节点。
n, q<=1e6
关键的问题是怎么把树节点的贡献独立掉,然后使用线性性
假装我们知道了这个树长什么样子
那么对于区间[l, r]
惊喜地发现被访问的节点数等于
与[l, r]相交的区间或严格包含[l, r] - 被[l, r]包含且非叶子 + 叶子数(即r - l + 1)
对于后两项我的理解如下
如果一个子树被完全覆盖 那么只会访问它的根
而在二叉树中 任意子树的叶子节点数 = 非叶子节点数 + 1
于是我们可以对树上的每个区间对每个询问分别计算贡献
然而问题是我们并不知道这棵树长什么样子
所以就要计算一个区间作为二叉树上节点的概率
如果一个序列如下
1 2 3 4 5 6 7
设"a|b"表示a,b之间的间隔
那么如果要[4, 5, 6]作为一个非叶子节点
那么"3|4","6|7"就要先被切掉
也就是说 如果将这n - 1个间隔编号为1 ~ n-1
那么它们的每个排列对应一种二叉树
那么刚刚的例子中,3,6就要在排列中排在4,5之前
这个概率是$ 2 * frac{1}{2} * frac{1}{3}$
区间[l, r]成为节点的概率$ 2 * frac{1}{r - l + 2} * frac{1}{r - l + 3}$
需要注意的是 如果区间左端为1或右端为n 那么只需要一侧在前即可
比如[1, x]成为节点的概率就是(frac{1}{x})
复杂度(O(n^2q))