陈老师搬书

【问题描述】

陈老师喜欢网购书籍,经常一次购它个百八十本,然后拿来倒卖,牟取暴利。前些天,高一的新同学来了,他便像往常一样,兜售他的书,经过一番口舌,同学们决定买他的书,但是陈老师桌上的书有三堆,每一堆都有厚厚的一叠,他要想个办法用最轻松的方式把书拿下来给同学们.但是你想逗一下陈老师，于是,请你设计一个最累的方式给他.

若告诉你这三堆分别有i,j,k本书,以及每堆从下到上书的重量.每次取书只能从任意一堆的最上面取,那么请你帮助他设计一个方案,让他花最大的力气取下所有书(陈老师别打我).

显然,每次取书,陈老师的体力消耗都会加大,这里用体力系数代表,取下第一本书时,体力系数为1,第二本时为2,依次类推,而每次体力消耗值则为体力系数和书的重量之积。

举个例子:

三堆书及重量如下

 

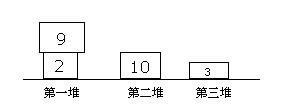
不用证明,最累的取书方式为: 右左左中, 即: 3*1+9*2+2*3+10*4=3+18+6+40=67

【输入文件】（book.in）

    输入文件的第一行为3个数,分别为三堆数量I,j,k

第二行至第四行分别为每堆由下至上的书本重量

【输出文件】（book.out）

    输出最累方式的体力消耗总值即可

【输入样例】   

3 2 4

2 3 2

1 5

9 8 7 4

【输出样例】   

257

【注释】:

输入数据为每堆由下至上的书本重量!

【数据规模】

对于40%的数据有:0<=i<10   0<=j<10   0<=k<10

对于100%的数据有:0<=i<100   0<=j<100   0<=k<100

最后输出的体力消耗总值在longint范围内

---

一眼望去眼里只有暴搜

• 40分的大暴力（无思路）

#include<stdio.h>
#include<algorithm>
using namespace std;
long long ans;
int k,w[4][101];

void dfs(int a,int b,int c,long long sum)
{
    if(a==0 && b==0 && c==0) {
        if(sum>ans) ans=sum;
        return ;
    }
    if(a) {
        ++k;
        dfs(a-1,b,c,sum+(k*w[1][a]));
        --k;
    }
    if(b) {
        ++k;
        dfs(a,b-1,c,sum+(k*w[2][b]));
        --k;
    }
    if(c) {
        ++k;
        dfs(a,b,c-1,sum+(k*w[3][c]));
        --k;
    }
}

int main()
{
    freopen("book.in","r",stdin);
    freopen("book.out","w",stdout);
    for(int i=1;i<=3;++i) {
        scanf("%d",&w[i][0]);
    }
    for(int i=1;i<=3;++i)
        for(int j=1;j<=w[i][0];++j) {
            scanf("%d",&w[i][j]);
        }
    
    dfs(w[1][0],w[2][0],w[3][0],0);
    printf("%lld",ans);
    return 0;
}

• 正解DP做法

F[i][j][k]表示目前第1堆剩余i本，第2堆剩余j本，第3堆剩余k本的最大劳累值

f[i][j][k]=max(max(f[i+1][j][k]+d[i+1]*t,f[i][j+1][k]+e[j+1]*t),f[i][j][k+1]+g[k+1]*t);

t=a+b+c-i-j-k

 其中a,b,c为3堆书本的数量，d[i],e[i],g[i]对应3堆书中第i本书的质量

#include<stdio.h>
#include<algorithm>
using namespace std;
int k[4],bok[4][101],f[101][101][101];

int main()
{
    freopen("book.in","r",stdin);
    freopen("book.out","w",stdout);
    for(int i=1;i<=3;++i)
        scanf("%d",&k[i]);
        
    for(int i=1;i<=3;++i) 
        for(int j=1;j<=k[i];++j)
            scanf("%d",&bok[i][j]);
    
    for(int i=k[1];i>=0;--i)
        for(int j=k[2];j>=0;--j)
            for(int l=k[3];l>=0;--l)
            {
                int t=k[1]+k[2]+k[3]-(i+j+l);
                f[i][j][l]=max(max(f[i+1][j][l]+bok[1][i+1]*t,f[i][j+1][l]+bok[2][j+1]*t),f[i][j][l+1]+bok[3][l+1]*t);
            } 
                            
    printf("%d",f[0][0][0]);
    return 0;            
}
/*
3 2 4
2 3 2
1 5
9 8 7 4    
*/