117. 填充每个节点的下一个右侧节点指针 II

<>

题目描述

---

给定一个二叉树

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：

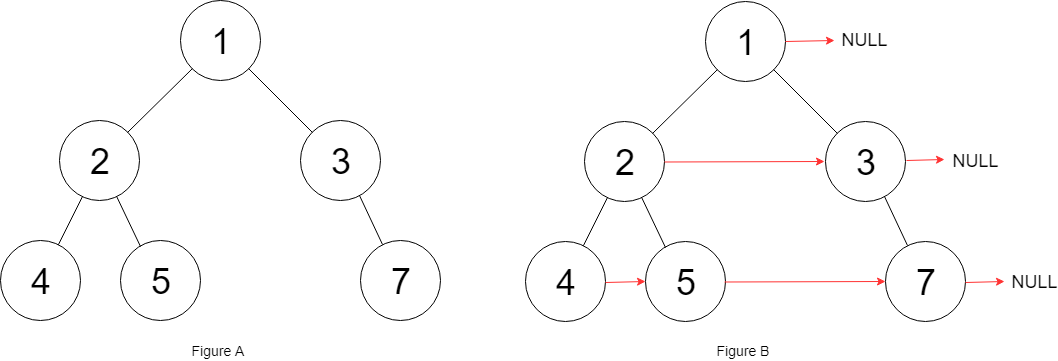
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

• 树中的节点数小于 6000
• -100 <= node.val <= 100

我的思路 - 递归

---

class Solution(object):
    def connect(self, root):
        """
        :type root: Node
        :rtype: Node
        """
        if not root:
            return 
        # 讨论左孩子的情况
        if root.left:
            # ①：当前结点有左右孩子
            if root.right:
                root.left.next = root.right
            else:
            # ②：只有左孩子，那么我们在当前结点这一层往next方向搜索
            #            直到找到符合答案的结点，没找到就是None
                layerNode = root.next
                while layerNode:
                    if layerNode.left:
                        root.left.next = layerNode.left
                        break
                    elif layerNode.right:
                        root.left.next = layerNodet.right
                        break                        
                    layerNode = layerNode.next
        # 讨论右孩子的情况
        if root.right:
            # 右孩子直接采用层序搜索（和上面的代码一样。。。）
            layerNode = root.next
            while layerNode:
                if layerNode.left:
                    root.right.next = layerNode.left
                    break
                elif layerNode.right:
                    root.right.next = layerNode.right
                    break
                layerNode = layerNode.next

        # 不能采用先左   后右的顺序
        self.connect(root.left)
        self.connect(root.right)        
        
        # 正确的应该先右  后左
        self.connect(root.right)        
        self.connect(root.left)
        
        return root

• 说明一下为什么不能采用先左后右的递归顺序

---------------------------------

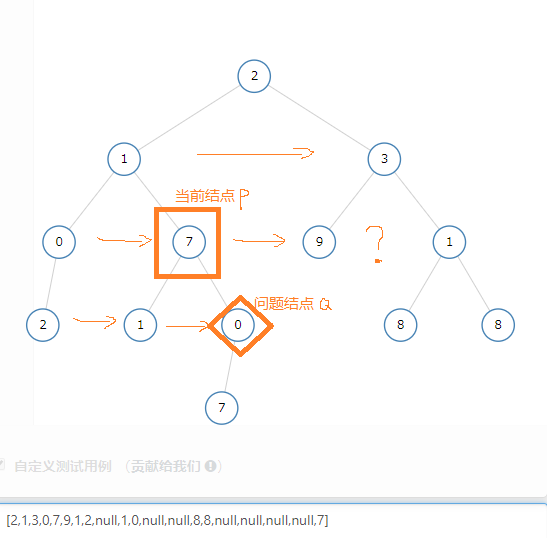
假设正处理到当前结点P，现在要为 P 的右孩子 Q 找到右侧结点 x，使得 Q.next = x

我们在当前结点P的这一层往next的方向走，找到了结点 9 ，一看这是个孤儿，于是还想继续往下。

可是这个孤儿 9 没有 next 的结点了，于是在这里断掉。

所以要采取先右  再左的递归策略。

 

• 改进的可能

  • 代码结构需要优化一下