题目如下:
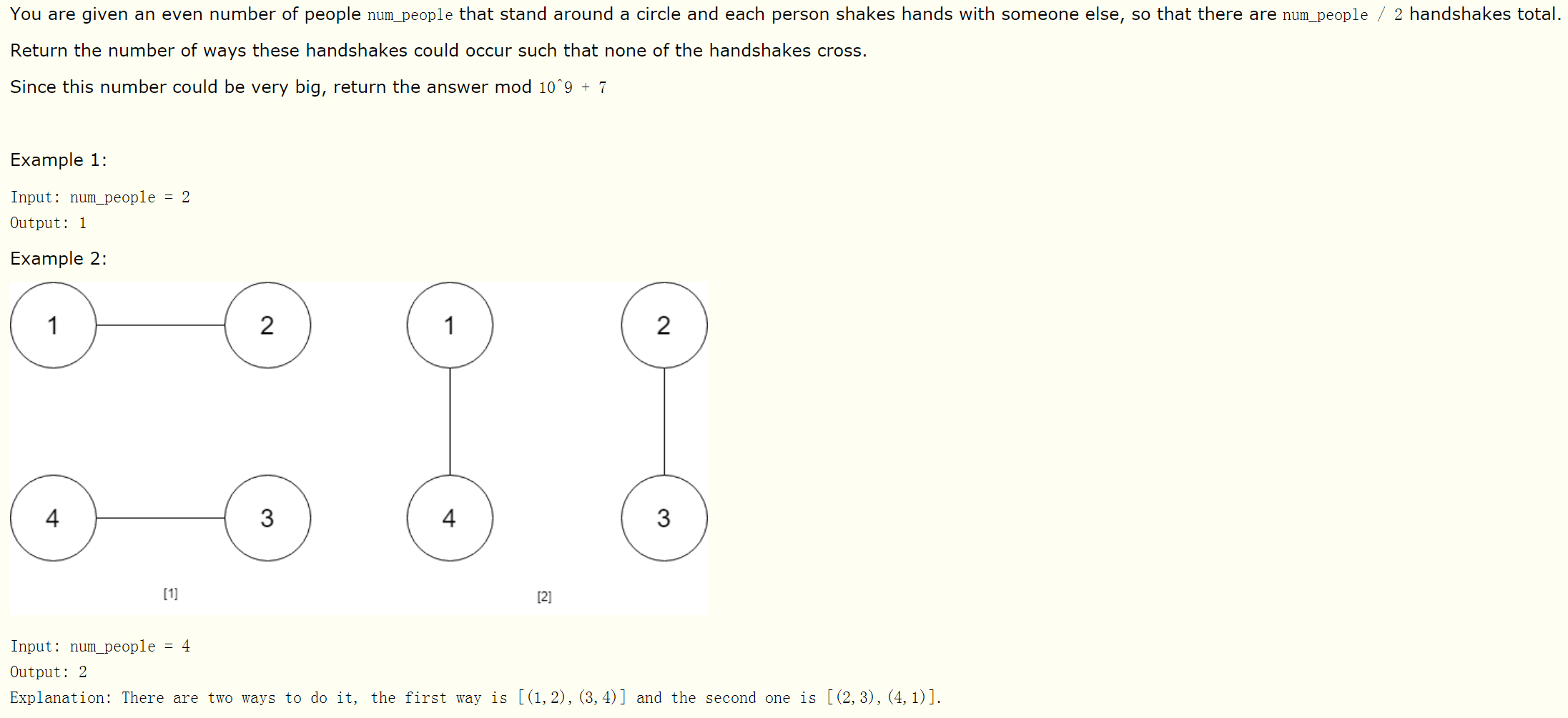

解题思路:动态规划。记dp[i] = v表示由i个人组成的圈子一共有v种握手的方法。对于一个由n个人组成的圈子,编号为0的人一共可以和编号为 (1,3,5....,n-1)的握手,这也很好理解,假设编号为0的人和编号为2的人握手,那么编号为1的人就被包在两人的连线的一侧,而同侧没有其他人可以握手。假设编号为0的人和编号为i的人握手,可以理解成0~i之间的连线把其余人分成了两部分,一部分的人编号是1~i-1,另外一部分的编号是i+1~n-1,这两部分分别形成独立的圈子,所以编号为0的人和编号为i的人握手时,可以握手的组合的总数就应该dp[i-1] * dp[n-i-1],最后只要累计编号为0的人分别和编号为 (1,3,5....,n-1)的总数即可。这里有一个例外,就是0和1握手或者0和n-1握手,这种方式并没有把剩余的人分成两个圈子,而是一个圈子。
代码如下:
class Solution(object): def numberOfWays(self, num_people): """ :type num_people: int :rtype: int """ num_people += 1 dp = [0] * (num_people) dp[2] = 1 for i in range(4,num_people,2): for j in range(2,i+1,2): left = (j - 1 - 1) right = (i - j) if left == 0: dp[i] += dp[right] elif right == 0: dp[i] += dp[left] else: dp[i] += dp[left] * dp[right] return dp[-1] % (10**9 + 7)