以前总不能理解坐标变换,自己不能很顺利的做推导,某晚上在看一本书时,突然开朗了。。
下面我来谈下自己的理解。
我们知道一个线性变换,是两个有乘和加操作的向量空间的函数,可以用一个变换矩阵来表示。
先以在R^2空间上几个简单变换为例:
我知道知道逆时针旋转\theta,可以用以下矩阵表示:
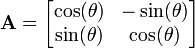
我们先从第一个角度出发看:点p = (x,y)^T旋转后坐标变为了 Ap, 注意此时的坐标系没什么变化,因此我们很容易理解。
但我们知道旋转是相对的,如果认为是坐标系发生了旋转呢?
这种情况下,方便表示令原坐标系为C,新坐标系为C’,我们知道的是p点在C中的坐标(x,y,z)。
还有呢?实际上我们还知道变换后的p(记为 p’)在C’中的坐标,也有 (x,y)
还有呢?旋转角度\theta
要求什么呢? p’在C中的坐标。
已知和所求清楚后,关键的地方来了,我们有了两个坐标架,现在假想我们站在C中看C’的三个标准轴 i’,j’,k’,则分别变为了Ai’ Aj’ Ak’
因此,对于p’ = (x,y,z)^T [in C’],其在C中的坐标应为p’ = A*p [in C]
下一篇文章中,以一个更复杂的例子分析,这是一个在机器人手臂或者说多关节的例子。