luogu板子传送
现在我们有许多许多矩形,并且我们知道每个矩形左上角和右下角的坐标,我们需要求这些矩形的面积并
扫描线的思路
假设我们现在只有两个矩形
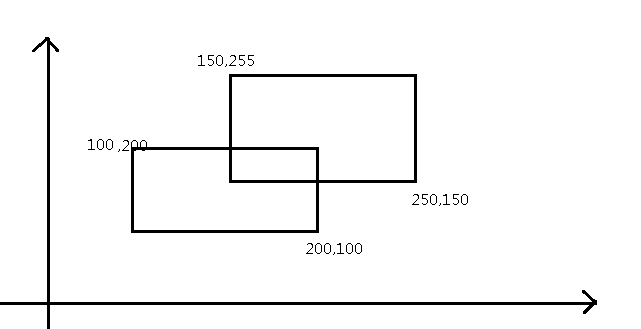
没错就是洛谷样例
我们假设有一条线从x轴开始,往上扫描,那这条线肯定会扫描到所有矩形的所有底边
我们把这些底边标出来

每两条底边之间,对答案的贡献肯定就是它们的高度差( imes)当前的底的长度
比如说,第一次就会将这一部分加入到答案里
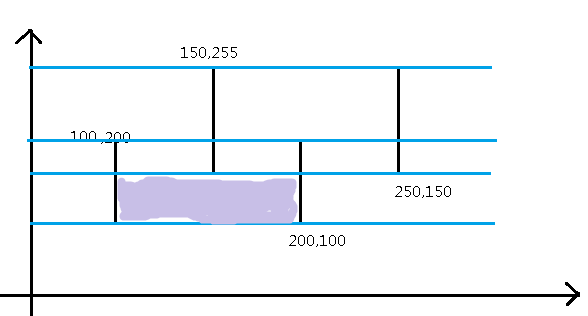
第二次就会将这一部分加入答案里

所以我们要做到就是维护底的长度
在上图中,我们注意到(x)可以被分成3个有用的部分,就像这样
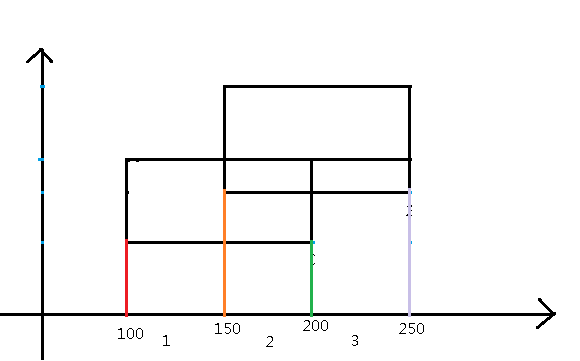
我们给每个部分设一个(cnt)值,来表示这个部分当前是否在要计算的底边里
当(cnt_i > 0)时,表示这个部分在里面,反之则不在
当前用来计算的底边的长度则为所有(cnt>0)的部分的长度之和
如果我们的扫描线扫描到的底边是下底,则其包含的部分的(cnt)都(+1)
若当前的扫描线是某个矩形的上底,则该矩形底边覆盖的部分的(cnt)值都-1
若当前(cnt_i>0),则说明(i)肯定被某个矩形的下底覆盖且当前扫描线还没有到达该矩形的上底,所以(i)肯定会被算到底边里
问题来了,我们应该怎么去实现呢?
我们观察一下上面的图,可以看到每个部分都是一条线段
同时,每个矩形的底边也是线段,并且会覆盖整数个部分
我们还要对这些覆盖的部分进行加减操作
很像线段树有木有?
所以我们用线段树来搞(cnt)的维护
线段树的搞法
我们先用(X)数组记录下所有的横坐标,然后离散化,此时(X[i])表示部分(i)的左端点的(x)值。
若不相同的(x)坐标一共有(m)个,则会有(m-1)个部分。我们在建线段树时,(cnt[l,r])表示第(l)个部分一直到第(r)个部分这个整体是否被完全覆盖((cnt>0)表示被完全覆盖)
为了快速得出所有(cnt>0)的区间的总长度,我们再用(sgt[l,r])表示从第(l)个部分一直到第(r)个部分中,(cnt>0)的区间总长度(注意上面的(cnt)要求全被覆盖,这里(sgt)可以有中间没有被覆盖的区间)。若(cnt[l,r]>0),则(sgt[l,r]=X[r+1]-X[l]),因为第(r)个部分的右端点是(X[r+1])
若([l,r])并没有完全被覆盖,则(sgt[l,r])由它的两个儿子更新而来
似乎就没什么可以口胡的了
来康康代码吧
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<map>
#include<cstdlib>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read()
{
char ch=getchar();
int x=0;bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-') f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return f?-x:x;
}
int n,cl,cx;
ll ans,sgt[1600009],wa[400009],cnt[1600009];//这里wa就是上文的X,以及注意开longlong
struct sl{
int y,xl,xr,d;//y记录当前扫描线纵坐标,xl为左端点,xr为右端点,d=1或-1,表示增加的cnt
}lin[400009];
bool cmp(sl a,sl b)
{
return a.y<b.y;
}
void add(int k,int l,int r,int x,int y,int d)
{
if(x<=l&&r<=y)
{
cnt[k]+=d;
if(cnt[k]>0) sgt[k]=wa[r+1]-wa[l];
else if(l==r) sgt[k]=0;//若当前区间只包含一个部分且未被覆盖,则总长度为0
else sgt[k]=sgt[k<<1]+sgt[k<<1|1];
return ;
}//由于cnt不能通过左右儿子更新,所以就没有pushdown了
int mid=(l+r)>>1;
if(x<=mid) add(k<<1,l,mid,x,y,d);
if(mid<y) add(k<<1|1,mid+1,r,x,y,d);
if(cnt[k]>0) sgt[k]=wa[r+1]-wa[l];
else if(l==r) sgt[k]=0;
else sgt[k]=sgt[k<<1]+sgt[k<<1|1];
}
int main()
{
n=read();int ccx=0;
for(int i=1;i<=n;i++)
{
int x1=read(),yy=read(),x2=read(),yyy=read();
lin[++cl].xl=x1;lin[cl].xr=x2;lin[cl].y=yy;lin[cl].d=1;
lin[++cl].xl=x1;lin[cl].xr=x2;lin[cl].y=yyy;lin[cl].d=-1;
wa[++ccx]=x1;wa[++ccx]=x2;
}
sort(wa+1,wa+ccx+1);
cx=unique(wa+1,wa+ccx+1)-wa-1;//cx相当于上述的m
sort(lin+1,lin+cl+1,cmp);
int h=0,sum=0;
for(int i=1;i<cl;i++)
{
h=lin[i].y;
int lft=lower_bound(wa+1,wa+cx+1,lin[i].xl)-wa;
int rgt=lower_bound(wa+1,wa+cx+1,lin[i].xr)-wa-1;//-1之后才是对应的第r个部分
add(1,1,cx-1,lft,rgt,lin[i].d);//总共有cx-1个部分
ans+=sgt[1]*(lin[i+1].y-lin[i].y);
}
printf("%lld
",ans);
}
来几道练手题叭(待补充)
窗口的星星