牛客2021年度训练联盟热身训练赛第一场（讲题）

E题: Early Orders

题意：给定 n ，k 和长度为n的数组x[i]

1<=k<=n<=2e5, 1<=x[i]<=k;

要在这个数组里找一个长度为k的子序列，使得数字1到k在这个序列里各出现一次，输出字典序最小的子序列

输入保证数组 x[i] 包括了1到k的所有数字

思路：很容易想到贪心地选择小的数放在前面，可以用单调栈来做

做法：

从左往右扫原数组，对于x[i]：

1、栈为空时，数字入栈；

2、栈非空，那么可以把栈里大于x[i]的数弹出，(从栈顶依次往下弹出) ，这样就维护了一个单调栈;

3、栈里存在数字x[i]，直接continue，就算栈里有比x[i]大的数也不弹出；(可以试试1 2 1 3 2这个样例，1不能把2弹出，否则1 2 3变成1 3 2)

4、栈里的某个数字在x[i+1]到x[n]都不存在，那么这个数就算比 x[i] 大，也不弹出这个数，就是说从栈顶弹出到这种数就不继续弹了

注释代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int MAXN = 2e5 + 7;
int a[MAXN];
int last[MAXN];
bool vis[MAXN];
int ans[MAXN];
int st[MAXN];//手写栈
int main()
{
	int n, k;
	cin >> n >> k;
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	int l = 0, r = 0;
	for (int i = 1; i <= k; i++) vis[i] = false;
	for (int i = 1; i <= n; i++) last[i] = false;
	for (int i = n; i; i--) {
		if (!vis[a[i]]) {
			vis[a[i]] = true;
			last[a[i]] = i;//数字a[i]在数组里最后一次出现的位置是last[a[i]]
		}
	}
	for (int i = 1; i <= k; i++) vis[i] = false;
	for (int i = 1; i <= n; i++) {
		if (vis[a[i]]) continue;//栈里有a[i]这个数字了，直接continue
		while (r != l && a[i] <= st[r] && i <= last[st[r]]) {//栈顶数字比a[i]大，同时还没有扫到栈顶数字最后一次出现的位置，就弹出栈顶
			vis[st[r]] = false;//栈顶数字被弹出，栈里面就没有这个数字了，把vis置为false
			r--;//弹出操作
		}
		st[++r] = a[i];//入栈操作
		vis[a[i]] = true;//在栈里面，vis置为true
	}
	printf("%d", st[1]);
	for (int i = 2; i <= k; i++) printf(" %d", st[i]);
	printf("
");
	return 0;
}

　　

如果觉的自己的代码没问题，但就是wa了，欢迎找我帮忙造反例

I题：Full Depth Morning Show

题意：给定一颗节点数为n的树，给定每个节点的点权 t[ i ] ，给定 n - 1条边（u,v,w），w为这条边的边权，用 f[u][v]表示从u到v的这条路径的花费

题目定义f[u][v] 为u到v的路径中所有边的边权之和乘以u,v的点权之和，用公式来表示就是f[u][v] = (Σw)* (t[ u ] + t[ v ])

总花费为所有从 非根节点 到 根节点 的路径的花费之和，即计算Σf[u][root] (u!=root)

在第一行输出以一号节点为根节点时，总共的花费

在第二行输出以二号节点为根节点时，总共的花费

。。。

一共输出n行

思路：

所有节点都要体验一遍当根节点的情况，那么可以考虑用换根dp，记dp[i]为以 i 节点为根节点的总贡献

怎么计算总花费，我们可以换个角度来计算，不把它看成是所有路径的贡献之和，而看成是所有边的贡献之和

考虑以一号节点为根节点，任选一条边，它的贡献怎么算，用 g[i] 表示一条边的贡献

如图：

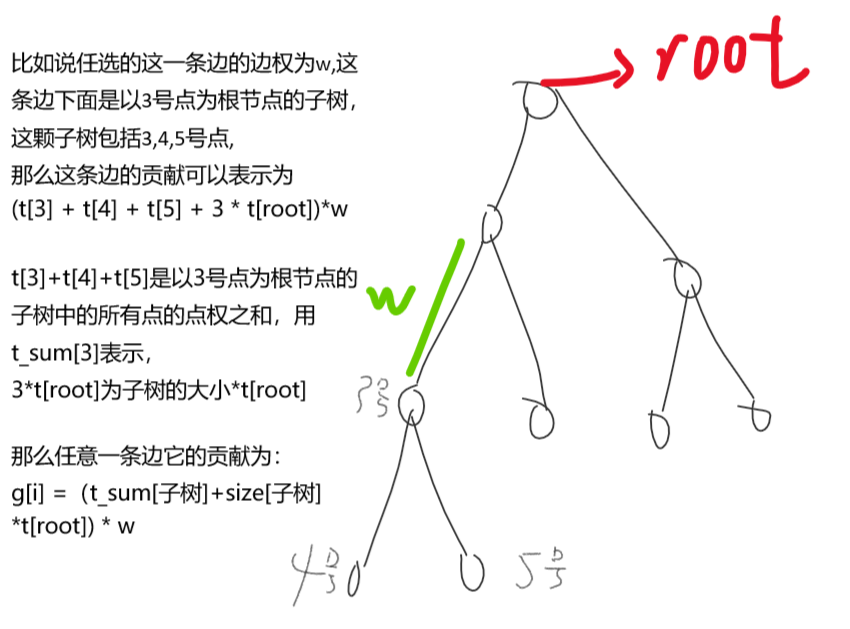
 这样我们得到了任意一条边的贡献为:g[ i ] = (t_sum[子树] + size[子树] * t[root] ) * w[ i ]

把所有边的贡献加起来就是总贡献:dp[root] = Σg[i]

我们一开始可以把这棵树以1号节点为根节点，先扫一遍，计算出分别以各个节点为根节点的子树，它的大小size[子树]，它的t_sum[子树]

然后再扫一遍，计算出以1号节点为根节点时，用计算出所有边的贡献并加起来的方法计算出总贡献

这两次扫描可以一起扫描

代码：

void dfs1(int s, int f) {
	siz[s] = 1; t_sum[s] += t[s];
	for (int i = head[s]; i; i = edge[i].next) {//这段是求每个节点的siz[]和t_sum[]
		int po = edge[i].to;
		if (po == f) continue;
		fa[po] = s;
		dfs1(po, s);
		siz[s] += siz[po];
		t_sum[s] += t_sum[po];
	}
	for (int i = head[s]; i; i = edge[i].next) {//这段是计算每条边的贡献并加起来
		int po = edge[i].to;
		if (po == fa[s]) continue;
		long long w = edge[i].cost;
		dp[1] += t_sum[po] * w;
		su += (long long)siz[po] * w;
	}
}

　　

dp[1] += su * t[1];

　　

这样我们得到了dp[1]，现在考虑dp数组怎么转移

dp[1] = Σg[i] = Σ(  (t_sum[子树] + size[子树] * t[1] ) * w[ i ]  )

设2号节点为1号节点的儿子节点

现把根节点从1号节点转移到2号节点

如图：

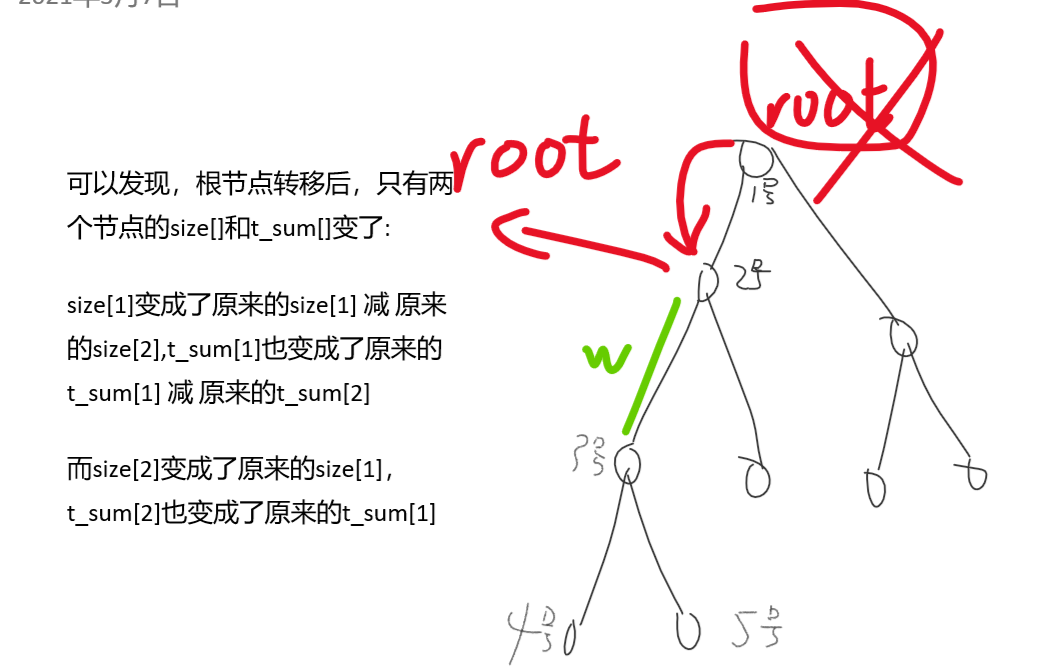
只有两个节点的t_sum[子树]和size[子树]改变了，同时对比以下这两项

dp[1] = Σg[i] = Σ(  (t_sum[子树] + size[子树] * t[1] ) * w[ i ]  )

dp[2] = Σg[i] = Σ(  (t_sum[子树] + size[子树] * t[2] ) * w[ i ]  )

由于只有两个节点的t_sum[子树]发生了变化，而所有size[子树]乘的t[1]变成了t[2]

所以我们把边的贡献拆成两项g[i] = t_sum[子树] * w[i] (第一项) + size[子树]*t[2]*w[i]（第二项）

可以发现，只有一条边的贡献的第一项发生了变化，而所有边的贡献的第二项发生了变化,但是第二项里的size[子树]*w[i]也是只有一条边发生了变化

如图：

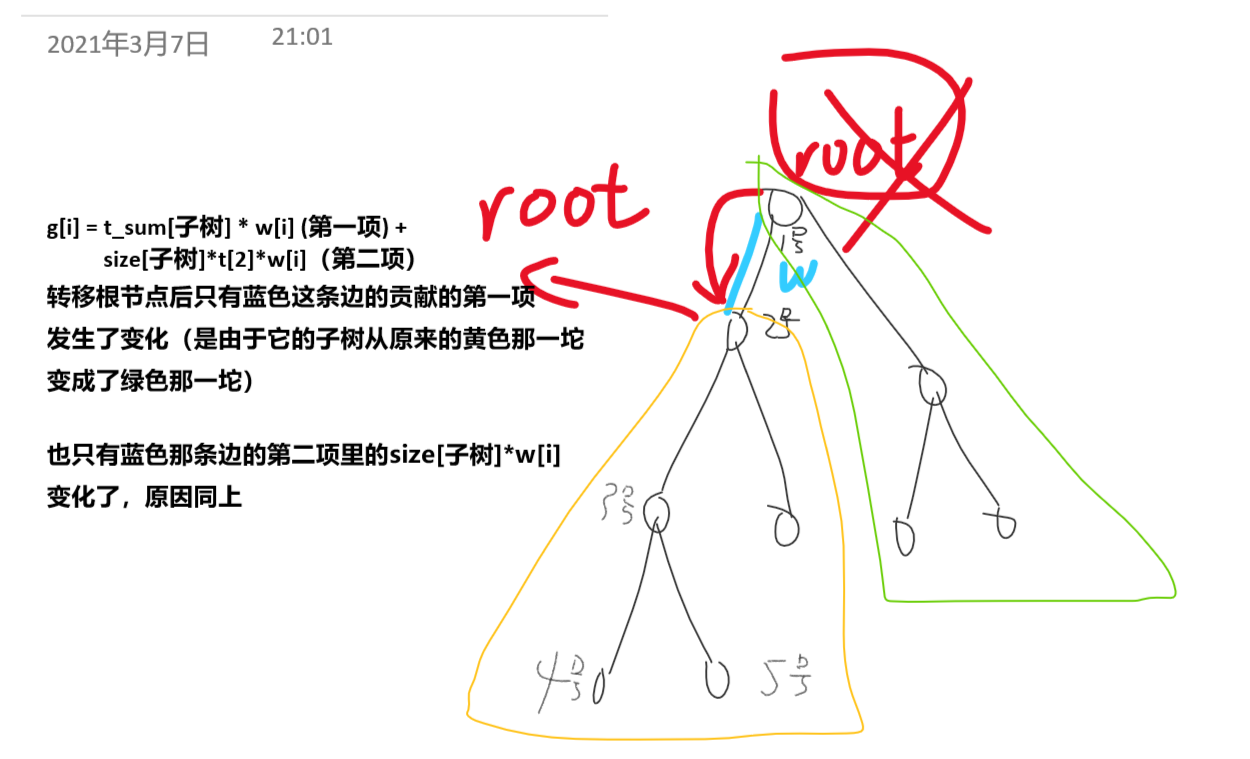
所以我们要分别来计算这两项的改变量

计算第一项的改变量，我们可以把改变了的那条边的第一项的改变量求出来

计算第二项的改变量，我们可以用su[i]表示以 i 为根节点时, Σsize[子树]*w[i]为多少: su[i] = Σsize[子树]*w[i] 。然后就好算了

能算出这两项改变量，就可以用dfs扫一遍来在树上算dp[i]了

dfs代码：

void dfs2(int s) {
	for (int i = head[s]; i; i = edge[i].next) {
		int po = edge[i].to;
		if (po == fa[s]) continue;
		long long w = edge[i].cost;
		dp[po] = dp[s] - (t_sum[po] * w) - su[s] * t[s];
		dp[po] += (t_sum[1] - t_sum[po]) * w;
		su[po] = su[s] - (long long)siz[po] * w;
		su[po] += ((long long)siz[1] - siz[po]) * w;
		dp[po] += su[po] * t[po];
		dfs2(po);
	}
}

　　

总的代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int MAXN = 2e5 + 7;
struct EDGE {
	int to, next;
	long long cost;
}edge[MAXN*2];
int head[MAXN], tot = 0;
void add(int u, int v, long long w) {
	tot++;
	edge[tot].to = v;
	edge[tot].cost = w;
	edge[tot].next = head[u];
	head[u] = tot;
}
long long dp[MAXN],t[MAXN],t_sum[MAXN],su[MAXN];
int siz[MAXN], fa[MAXN];
void dfs1(int s, int f) {
	siz[s] = 1; t_sum[s] += t[s];
	for (int i = head[s]; i; i = edge[i].next) {//这段是求每个节点的siz[]和t_sum[]
		int po = edge[i].to;
		if (po == f) continue;
		fa[po] = s;
		dfs1(po, s);
		siz[s] += siz[po];
		t_sum[s] += t_sum[po];
	}
	for (int i = head[s]; i; i = edge[i].next) {//这段是计算每条边的贡献并加起来
		int po = edge[i].to;
		if (po == fa[s]) continue;
		long long w = edge[i].cost;
		dp[1] += t_sum[po] * w;
		su[1] += (long long)siz[po] * w;
	}
}
void dfs2(int s) {
	for (int i = head[s]; i; i = edge[i].next) {
		int po = edge[i].to;
		if (po == fa[s]) continue;
		long long w = edge[i].cost;
		dp[po] = dp[s] - (t_sum[po] * w) - su[s] * t[s];
		dp[po] += (t_sum[1] - t_sum[po]) * w;
		su[po] = su[s] - (long long)siz[po] * w;
		su[po] += ((long long)siz[1] - siz[po]) * w;
		dp[po] += su[po] * t[po];
		dfs2(po);
	}
}
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		scanf("%lld", &t[i]);
	}
	int u, v; long long w;
	for (int i = 1; i <= n - 1; i++) {
		scanf("%d%d%lld", &u, &v, &w);
		add(u, v, w);
		add(v, u, w);
	}
	dfs1(1, 0);
	dp[1] += su[1] * t[1];
	dfs2(1);
	for (int i = 1; i <= n; i++) {
		printf("%lld
", dp[i]);
	}
	return 0;
}

　　

有许多树上的题都是这种二次dfs扫描，考虑换根后的改变量